
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبر
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبردرباره من
دستهها
- تصاویر جالب علمی 60
- اخبار علمی 116
- تاریخ علم 21
- مقالات علمی 187
- حقایق علمی 29
- پرسش و پاسخ علمی 4
- تکنولوژی نظامی 170
- مشاهیر 11
- معرفی وبسایت علمی 10
- سخن بزرگان 4
- تفریح و سرگرمی 1
- شگفتیهای طبیعت 6
- مسابقه علمی 6
- زبان انگلیسی 18
- دیرین شناسی 35
- مهندسی مکانیک 56
- دنیای ریاضیات 54
- فایل های قابل دانلود 8
- پزشکی و سلامت 88
- ترین ها 38
- کنکور 1390 14
- نمونه سوال امتحانی و آزمون 20
- معرفی نرم افزار 4
- واژه نامههای تخصصی 1
- آزمایش های ساده و جالب فیزیک 4
- کنکور 13
- تکنولوژی نفت و حفاری 5
- بانک مقالات علمی 3
- آیرودینامیک و پرواز 6
- استانداردهای مهندسی 6
- محیط زیست 39
- باستان شناسی 5
- پروژه درسی و سمینار 5
- برنامه نویسی کامپیوتر 11
- رپرتاژ آگهی 1
ابر برجسب
کووید 19 کرونا ویروس ریاضیات جنگنده هواپیما ستاره زمین لرزه گرمایش جهانی F-35 موشک کنکور بمب افکن سیاهچاله جنگ جهانی دومبرگهها
جدیدترین یادداشتها
همه- کوارک ها: اجزای سازنده ماده
- آموزش زبان برنامه نویسی پایتون با مثال
- سمی ترین حیوانات طبیعت
- کهن ترین مجسمه ساخت انسان
- راه حل اویلر برای مساله بازل
- ژنتیک: چگونه ویژگیهای خود را از نیاکان به ارث میبریم؟
- برنارد ریمان، آفریدگار هندسه نا اقلیدسی
- ابتذال چیست؟ ریشه آن کدام است؟
- اتمها از کجا آمدهاند؟
- پیری: با گذشت عمر چه اتفاقی برای بدن می افتد؟
- مسایل حل شده از معادلات دیفرانسیل
- لئونارد اویلر
- بخشهای مختلف هواپیما و کارکرد آنها
- انسان بر لبه انقراض
- ساخت بزرگترین هواپیمای حامل پهباد توسط چین
بایگانی
- آبان 1404 2
- مهر 1404 3
- شهریور 1404 3
- مرداد 1404 2
- تیر 1404 2
- خرداد 1404 3
- اردیبهشت 1404 1
- فروردین 1404 1
- اسفند 1403 1
- بهمن 1403 2
- دی 1403 1
- آذر 1403 1
- مهر 1403 1
- شهریور 1403 3
- مرداد 1403 1
- تیر 1403 3
- خرداد 1403 4
- اردیبهشت 1403 3
- فروردین 1403 2
- اسفند 1402 7
- بهمن 1402 2
- دی 1402 3
- آذر 1402 3
- آبان 1402 2
- مهر 1402 5
- شهریور 1402 4
- مرداد 1402 12
- تیر 1402 12
- خرداد 1402 5
- اردیبهشت 1402 6
- فروردین 1402 8
- اسفند 1401 6
- بهمن 1401 9
- دی 1401 2
- آذر 1401 3
- آبان 1401 1
- مهر 1401 1
- شهریور 1401 4
- مرداد 1401 7
- تیر 1401 12
- خرداد 1401 10
- اردیبهشت 1401 12
- فروردین 1401 4
- اسفند 1400 4
- بهمن 1400 7
- دی 1400 2
- آبان 1400 5
- مهر 1400 9
- شهریور 1400 1
- مرداد 1400 3
- تیر 1400 6
- خرداد 1400 7
- اردیبهشت 1400 8
- فروردین 1400 7
- اسفند 1399 12
- بهمن 1399 11
- دی 1399 1
- آذر 1399 7
- آبان 1399 2
- مهر 1399 1
- اردیبهشت 1399 7
- فروردین 1399 33
- اسفند 1398 13
- بهمن 1398 9
- دی 1398 1
- خرداد 1398 4
- اردیبهشت 1398 7
- بهمن 1397 5
- دی 1397 5
- آذر 1397 2
- آبان 1397 3
- مهر 1397 3
- شهریور 1397 1
- مرداد 1397 7
- تیر 1397 7
- خرداد 1397 2
- اردیبهشت 1397 6
- اسفند 1396 3
- بهمن 1396 5
- دی 1396 4
- آذر 1396 8
- آبان 1396 6
- مهر 1396 5
- شهریور 1396 6
- مرداد 1396 10
- تیر 1396 9
- خرداد 1396 5
- اردیبهشت 1396 3
- فروردین 1396 8
- اسفند 1395 3
- بهمن 1395 3
- دی 1395 1
- آذر 1395 4
- آبان 1395 2
- مهر 1395 7
- شهریور 1395 5
- مرداد 1395 1
- تیر 1395 3
- خرداد 1395 1
- اردیبهشت 1395 1
- فروردین 1395 3
- اسفند 1394 8
- بهمن 1394 2
- دی 1394 1
- آذر 1394 3
- آبان 1394 2
- مهر 1394 1
- مرداد 1394 1
- تیر 1394 2
- فروردین 1394 1
- اسفند 1393 4
- بهمن 1393 2
- دی 1393 1
- آبان 1393 1
- شهریور 1393 1
- مرداد 1393 1
- تیر 1393 3
- اردیبهشت 1393 7
- فروردین 1393 1
- اسفند 1392 2
- بهمن 1392 8
- دی 1392 6
- آذر 1392 16
- آبان 1392 14
- مهر 1392 19
- شهریور 1392 17
- مرداد 1392 6
- تیر 1392 2
- خرداد 1392 5
- اردیبهشت 1392 9
- فروردین 1392 1
- اسفند 1391 5
- بهمن 1391 8
- دی 1391 6
- آذر 1391 8
- آبان 1391 5
- مهر 1391 12
- شهریور 1391 7
- مرداد 1391 2
- تیر 1391 6
- خرداد 1391 7
- اردیبهشت 1391 8
- فروردین 1391 13
- اسفند 1390 7
- بهمن 1390 6
- دی 1390 11
- آذر 1390 2
- آبان 1390 6
- مهر 1390 4
- شهریور 1390 5
- مرداد 1390 8
- تیر 1390 15
- خرداد 1390 25
- اردیبهشت 1390 11
- فروردین 1390 1
- اسفند 1389 13
- بهمن 1389 12
- دی 1389 5
- آذر 1389 3
- آبان 1389 6
- مهر 1389 7
- شهریور 1389 6
- خرداد 1389 1
- اردیبهشت 1389 3
- اسفند 1388 7
- بهمن 1388 10
- دی 1388 11
- آذر 1388 7
- آبان 1388 17
- آذر 1387 1
- آبان 1387 9
- مهر 1387 5
- شهریور 1387 1
- مرداد 1387 3
- تیر 1387 7
- خرداد 1387 5
- اردیبهشت 1387 1
- فروردین 1387 3
- اسفند 1386 3
- بهمن 1386 9
- دی 1386 19
- آذر 1386 19
- آبان 1386 7
تقویم
آبان 1404| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
جستجو
آخرین قضیه فرما
پیر فرما (تولد 1601) بنیان گذار نظریه نوین اعداد محسوب می شود. سالهایی از دهه 1630 زندگی او وقف تصحیح کتاب آریثماتیکا اثر کلاسیک دیوفانتوس شده بود. او در حاشیه این کتاب مطلبی یادداشت کرد که به مدت چهارصدسال ریاضی دانان پس از خود را به تکاپو واداشت.
این مطلب پیرامون قضیه ای بود که اکنون به عنوان آخرین قضیه فرما شناخته می شود. مطابق این قضیه معادله دیوفانتین یعنی 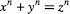 برای n > 2 در مجموعه اعداد صحیح جواب ندارد. به عنوان مثال هیچ سه عدد صحیح مخالف صفر را نمیتوان یافت که معادله x3 + y3 = z3 را برآورده سازد.
برای n > 2 در مجموعه اعداد صحیح جواب ندارد. به عنوان مثال هیچ سه عدد صحیح مخالف صفر را نمیتوان یافت که معادله x3 + y3 = z3 را برآورده سازد.
توجه کنید که برای n=2 معادله به فرم x2+y2 = z2 در میآید که همان قضیه فیثاغورث است و می دانیم بیشمار سه تایی صحیح میتوان پیدا کرد که در معادله فوق صدق کنند.
فرما در حاشیه کتاب ادعا کرد که اثبات این قضیه را یافته است. لیکن از ذکر آن خودداری کرد. اکنون تقریبا مطمئنیم که ادعای فرما خیلی دقیق نبوده و احتمالا برای n=3 و n=4 این قضیه را ثابت کرده، لیکن حل عمومی آن را نیافته است.
در سال 1993 انفجاری در عالم ریاضیات اتفاق افتاد. اندرو وایلز با اثبات حالت نیمه پایدار حدس تانی یاما-شیمورا قضیه فرما را بطور پارهای اثبات کرد. متاسفانه رخنههای متعددی در روش اثبات اندرو وایلز پدیدار شد. لیکن در سال 1994 وایلز و تایلور با همکاری هم مسئله را به یک فرمول شماره رده (Class Number Forula) فرو کاسته و اثبات نهایی آخرین قضیه فرما را ارائه کردند.
اثبات قضیه فرما پایان یک دوران در ریاضیات بود. از آن جایی که ابزارهای مورد استفاده در حل این مسئله هنوز در زمان فرما ابداع نشده بودند، بنظر می رسد حل ادعایی فرما واقعیت نداشته باشد.
در یکی از اپیزودهای کارتون معروف The Simpsons، معادله 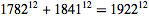 در نقطه ای از پس زمینه تصویر دیده می شود. ممکن است بنظر برسد که این اعداد به ازای n=12 در قضیه فرما صدق میکنند، در حالی که حاصل دو طرف تنها در نه رقم اول با یکدیگر تطابق دارد.
در نقطه ای از پس زمینه تصویر دیده می شود. ممکن است بنظر برسد که این اعداد به ازای n=12 در قضیه فرما صدق میکنند، در حالی که حاصل دو طرف تنها در نه رقم اول با یکدیگر تطابق دارد.

منابعی برای مطالعه بیشتر:
http://mathworld.wolfram.com/FermatsLastTheorem.html
حدس گولدباخ
به تساویهای زیر دقت کنید:
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7
12 = 5 + 7
14 = 7 + 7
16 = 5 + 11
18 = 7 + 11
20 = 7 + 13
22 = 5 + 17
24 = 7 + 17
...
به نظر می رسد هر عدد زوج بزرگتر از 2 را میتوان بصورت مجموع دو عدد اول نوشت. آیا این امر برای تمام اعداد زوج بزرگتر از 2 امکان پذیر است؟ اولین بار کریستین گولدباخ دانشمند نظریه اعداد (1690 تا 1764 میلادی) این نظریه را مطرح کرد. تلاش دانشمندان برای اثبات این مسئله هنوز به نتیجه نرسیده است!
دو قلوهای اول
دوقلوهای اول یا prime twines ، یک جفت عدد اول هستند که 2 واحد با یکدیگر تقاوت دارند. چند مثال از این جفت اعداد عبارتند از (3,5)، (11,13) و (1000000007,1000000009). بزرگترین دو قلوی اول شناخته شده عبارتند از:
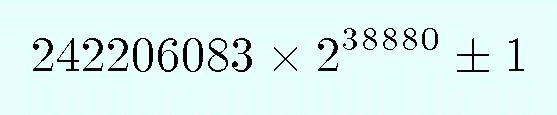
هرکدام از اعداد فوق 11713 رقم دارند. چه تعداد از این جفت اعداد اول وجود دارد؟ آیا تعداد این جفت اعداد اول محدود است یا نامحدود؟ هنوز کسی پاسخ این پرسشها را نمیداند!
منبع:
اعداد دوستدار هم یا متحابه
تالیف: اصغر ناصری
یک جقت اعداد دوستدار هم، دو عدد صحیح هستند که مجموع مقسوم علیه های سره یکی (مقسوم علیه های عدد غیر از خودش) با عدد دیگر برابر شود. کوچکترین جفت شناخته شده از این اعداد عبارتند از 220 و 284.
مجموع مقسوم علیه های عدد 220 عبارتند از:
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
و مجموع مقسوم علیه های 284 عبارتند از:
1 + 2 + 4 + 71 + 142 = 220
نه جفت از اولین اعداد دوستدار هم عبارتند از:
220, 284), (1184, 1210), (2620, 2924) (5020, 5564), (6232, 6368), (10744, 10856), (12285, 14595), (17296, 18416), (63020, 76084)
تاکنون حدود 5001 جفت از این اعداد شناخته شده و این بررسی تا عددی به بزرگی 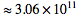 انجام شده است. یک جفت بزرگ از این اعداد عبارتند از:
انجام شده است. یک جفت بزرگ از این اعداد عبارتند از:
(2068113162038, 2101813493962)
بزرگترین جفت عدد دوستدار شناخته شده هرکدام 24073 رقم دارند و در سال 2005 توسط جابلینگ کشف شده اند. این اعداد با معادلات زیر معرفی می شوند:
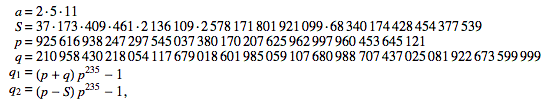
دو عدد کامل فوق بصورت زیر با استفاده از پارامترهای بالا بدست می آیند:
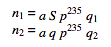
برای مطالعه بیشتر به منبع زیر مراجعه کنید:
اعداد کامل
تالیف: اصغر ناصری
ریاضیات علمی است پر از شگفتی. یونانیان باستان معتقد به وجود خواص جادویی و رموز نهفته در برخی اعداد و دنبالههای عددی بودند. آنچه آنان با به این فکر انداخته بود، نظم و پیوستگی حیرت انگیزی است که در جای جای ریاضیات به چشم می خورد. در این مقاله با اعداد کامل آشنا میشویم.
یک عدد کامل (perfect number) عددی است که با مجموع مقسوم علیههای خود (به غیر از خود عدد) برابر می باشد. کوچکترین عدد کامل عبارت است از ٦، زیر داریم:
6 = 1 + 2 + 3
اعداد کامل بعدی عبارتند از:
28 = 1 + 2 + 4 + 7 + 14
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
8128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064
اولین بار اقلیدس در کتاب خود به نام اصول به این اعداد اشاره کرده است. اقلیدس این قضیه جالب را نیز در مورد اعداد کامل بیان کرده است:
اگر برای K>1 عدد 2k-1 اول باشد، آنگاه 2k-1(2k-1) یک عد کامل است.
به عنوان مثال 23-1=7 یک عدد اول است، بنابراین 23-1(23-1)=4*7=28 باید یک عد کامل باشد که صحیح است.
همچنین 25-1=32-1=31 نیز یک عدد اول است. بنابراین 25-1(25-1)=16*31=496 نیز باید عددی کامل باشد که باز هم صحیح است.
چند عدد کامل بعدی عبارتند از:
33550336
8589869056
137438691328
2305843008139952128
چند خاصیت جالب دیگر اعداد کامل
رابطه بین اعداد کامل و اعداد مثلثی - تمام اعداد کامل بزرگتر از 6 شکل زیر را دارند:
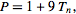
که Tn یک عدد مثلثی به شکل زیر است:
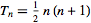
اعداد مثلثی اعدادی هستند که می توان آنها را به شکل آرایههای مثلثی نشان داد. شکل زیر دنباله اعداد مثلثی را نشان می دهد:

به عنوان مثال 28 یک عدد کامل است که می توان آن را به شکل 3*9 + 1 = 28 نوشت. همانطور که می بینید 3 یک عدد مثلثی است. به همین ترتیب 55*9 + 1 = 496 یک عدد کامل است و 55 نیز یک عدد مثلثی به ازای n = 10 است.
رابطه بین اعداد کامل و اعداد اول مرسین - به مجموع های زیر دقت کنید:
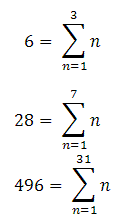
که 6 ، 7 ، 31 ، ... اعداد اول مرسین هستند. اعداد اول مرسین، اعداد اولی به شکل زیر هستند:
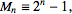
که n از دنباله اعداد زیر انتخاب می شود:
n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, ...
مجموع معکوس های مقسوم علیه های هر عدد کامل (خود عدد را نیز به حساب آورید) برابر 2 می شود. مانند:
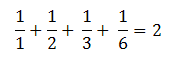
آیا هیچ عدد کامل فردی وجود دارد؟
تاکنون تمامی اعداد کامل شناخته شده زوج بوده اند و هیچ عدد فرد کاملی شناخته نشده است. این بررسی تا عدد 10 به توان 300 که عدد بسیار بزرگی است انجام شده است. لیکن دلیلی برای اثبات اینکه عدد فرد کامل وجود ندارد نیز بدست نیامده است. در وب سایت http://www.oddperfect.org پروژه ای در دست انجام است که هدف آن یافتن یک عدد فرد کامل می باشد.
برای مطالعه بیشتر درباره این اعداد شگفت انگیز، به منابع زیر مراجعه کنید:
Perfect Number, http://mathworld.wolfram.com/PerfectNumber.html
Perfect numbers,
http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Perfect_numbers.html