اتحادهای مثلثاتی

نمونه مسایل اتحادها و روابط مثلثاتی، قابل استفاده برا ی دانش آموزان دبیرستان

لینک دانلود فایل مقاله

---

تدریس ریاضیات دبیرستان و دانشگاه

توسط مدرس خصوصی مجرب با بیش از 25 سال سابقه تدریس

تدریس، حل تمرین، مشاوره

شماره تماس: [phone]

(ناصری)

---

سری های مثلثاتی و نحوه محاسبه آنها

سری های مثلثاتی مبحث بسیار جالبی در مثلثات پایه است که با وجود اهمیت و کاربرد انها در مباحث فیزیک دانشگاه، از کتابهای نظام جدید آموزش نظام جدید متوسطه حذف شده است. این نوشتار به معرفی چند سری مثلثاتی و شیوه محاسبه مجموع آنها برای دانش |آموزان علاقمند به ریاضی می پردازد.

->  دانلود متن کامل مقاله

---

تدریس دروس ریاضیات دبیرستان و دانشگاه

مدرس مجرب با بیش از 25 سال سابقه تدریس خصوصی

شماره تماس: [phone]

ناصری

---

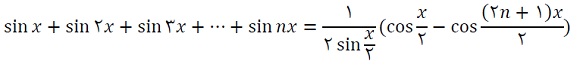
آماده شدن برای امتحان حسابان 2

مجموعه آخرین گام ها برای آماده شدن جهت امتحان پایان سال تدوین شده است. این مجموعه که حل تشریحی و مفصل سوالات مهم پایان سال است، می تواند به عنوان آخرین و مهم ترین گامهای لازم برای آماده شدن جهت امتحان در ساعات پایانی مورد استفاده قرار گیرد. جهت دانلود آخرین گامها برای حسابان 2 روی تصویر زیر کلیک کنید.

پوش یک دسته منحنی و طریقه یافتن آن (2)

برای قسمت اول این مقاله کلیک کنید.

مثال: پوش دسته منحنی زیر را بیابید:

(x-c)²+y²=9

---

َAdvertisement

---

حل - این دسته منحنی معرف دوایری به مرکز نقطه (c,0) و شعاع 3 است. برای بدست آوردن پوش دستگاه زیر را حل می کنیم:

f(x,y)=(x-c)²+y²-9=0

f_c(x,y)=2(x-c)=0 ->  x=c

در معادله دوم نسبت به c مشتق گرفته شده است. اگر در معادله دایره قرار دهیم x=c خواهیم داشت:

(c-c)²+y²=9->y=3  ,   y=-3

دو خط افقی مزبور معادلات پوش دسته منحنی هستند.شکل زیر نمودار دسته منحنی و پوش آن را نشان می دهد.

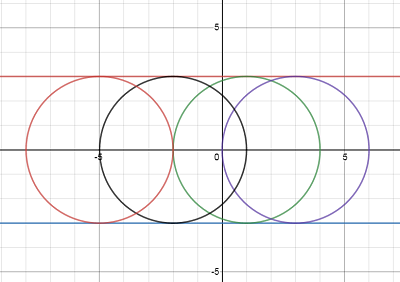
برای ترسیم این نمودار از نرم افزارآانلاین بسیار جالب سایت https://www.desmos.com/calculator استفاده شده است.

حل معادلات دیفرانسیلی که در آن x تابعی از مشتق اول y است.

حل معادلات دیفرانسیل به شکل x=f(y')

معادلاتی از این دست را به سادگی می توان با تغییر متغیر y'=u حل کرد. گاهی اوقات بهتر است 'y را معادل تابعی از u بگیریم. مثال: