
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبر
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبردرباره من
دستهها
- تصاویر جالب علمی 60
- اخبار علمی 115
- تاریخ علم 21
- مقالات علمی 183
- حقایق علمی 29
- پرسش و پاسخ علمی 4
- تکنولوژی نظامی 170
- مشاهیر 10
- معرفی وبسایت علمی 10
- سخن بزرگان 4
- تفریح و سرگرمی 1
- شگفتیهای طبیعت 6
- مسابقه علمی 6
- زبان انگلیسی 18
- دیرین شناسی 34
- مهندسی مکانیک 56
- دنیای ریاضیات 51
- فایل های قابل دانلود 8
- پزشکی و سلامت 88
- ترین ها 36
- کنکور 1390 14
- نمونه سوال امتحانی و آزمون 20
- معرفی نرم افزار 4
- واژه نامههای تخصصی 1
- آزمایش های ساده و جالب فیزیک 4
- کنکور 13
- تکنولوژی نفت و حفاری 5
- بانک مقالات علمی 3
- آیرودینامیک و پرواز 6
- استانداردهای مهندسی 6
- محیط زیست 38
- باستان شناسی 5
- پروژه درسی و سمینار 5
- برنامه نویسی کامپیوتر 10
- رپرتاژ آگهی 1
ابر برجسب
جنگنده هواپیما ریاضیات ستاره زمین لرزه گرمایش جهانی F-35 سیاهچاله جنگ جهانی دوم موشک کنکور بمب افکن کرونا کووید 19 ویروسبرگهها
جدیدترین یادداشتها
همه- لئونارد اویلر
- بخشهای مختلف هواپیما و کارکرد آنها
- انسان بر لبه انقراض
- ساخت بزرگترین هواپیمای حامل پهباد توسط چین
- چرا تمامی اشکال حیات به اکسیژن وابسته هستند؟
- رایانش کوانتومی چیست؟
- فیلها: بزرگترین حیوانات خشکی
- کاربرد هوش مصنوعی در حل مسایل علمی با Deepseek
- اورکا فرمانروای اقیانوس
- روباتهای انسان نما
- تاریخچه ابداع و ساخت خودرو
- آخرین نئاندرتال
- مروری بر سبک های مختلف نقاشی
- نوآوری در حل تست های ریاضی
- بازی بزرگان: برزیل و فرانسه جام جهانی 1986
بایگانی
- تیر 1404 1
- خرداد 1404 3
- اردیبهشت 1404 1
- فروردین 1404 1
- اسفند 1403 1
- بهمن 1403 2
- دی 1403 1
- آذر 1403 1
- مهر 1403 1
- شهریور 1403 3
- مرداد 1403 1
- تیر 1403 3
- خرداد 1403 4
- اردیبهشت 1403 3
- فروردین 1403 2
- اسفند 1402 7
- بهمن 1402 2
- دی 1402 3
- آذر 1402 3
- آبان 1402 2
- مهر 1402 5
- شهریور 1402 4
- مرداد 1402 12
- تیر 1402 12
- خرداد 1402 5
- اردیبهشت 1402 6
- فروردین 1402 8
- اسفند 1401 6
- بهمن 1401 9
- دی 1401 2
- آذر 1401 3
- آبان 1401 1
- مهر 1401 1
- شهریور 1401 4
- مرداد 1401 7
- تیر 1401 12
- خرداد 1401 10
- اردیبهشت 1401 12
- فروردین 1401 4
- اسفند 1400 4
- بهمن 1400 7
- دی 1400 2
- آبان 1400 5
- مهر 1400 9
- شهریور 1400 1
- مرداد 1400 3
- تیر 1400 6
- خرداد 1400 7
- اردیبهشت 1400 8
- فروردین 1400 7
- اسفند 1399 12
- بهمن 1399 11
- دی 1399 1
- آذر 1399 7
- آبان 1399 2
- مهر 1399 1
- اردیبهشت 1399 7
- فروردین 1399 33
- اسفند 1398 13
- بهمن 1398 9
- دی 1398 1
- خرداد 1398 4
- اردیبهشت 1398 7
- بهمن 1397 5
- دی 1397 5
- آذر 1397 2
- آبان 1397 3
- مهر 1397 3
- شهریور 1397 1
- مرداد 1397 7
- تیر 1397 7
- خرداد 1397 2
- اردیبهشت 1397 6
- اسفند 1396 3
- بهمن 1396 5
- دی 1396 4
- آذر 1396 8
- آبان 1396 6
- مهر 1396 5
- شهریور 1396 6
- مرداد 1396 10
- تیر 1396 9
- خرداد 1396 5
- اردیبهشت 1396 3
- فروردین 1396 8
- اسفند 1395 3
- بهمن 1395 3
- دی 1395 1
- آذر 1395 4
- آبان 1395 2
- مهر 1395 7
- شهریور 1395 5
- مرداد 1395 1
- تیر 1395 3
- خرداد 1395 1
- اردیبهشت 1395 1
- فروردین 1395 3
- اسفند 1394 8
- بهمن 1394 2
- دی 1394 1
- آذر 1394 3
- آبان 1394 2
- مهر 1394 1
- مرداد 1394 1
- تیر 1394 2
- فروردین 1394 1
- اسفند 1393 4
- بهمن 1393 2
- دی 1393 1
- آبان 1393 1
- شهریور 1393 1
- مرداد 1393 1
- تیر 1393 3
- اردیبهشت 1393 7
- فروردین 1393 1
- اسفند 1392 2
- بهمن 1392 8
- دی 1392 6
- آذر 1392 16
- آبان 1392 14
- مهر 1392 19
- شهریور 1392 17
- مرداد 1392 6
- تیر 1392 2
- خرداد 1392 5
- اردیبهشت 1392 9
- فروردین 1392 1
- اسفند 1391 5
- بهمن 1391 8
- دی 1391 6
- آذر 1391 8
- آبان 1391 5
- مهر 1391 12
- شهریور 1391 7
- مرداد 1391 2
- تیر 1391 6
- خرداد 1391 7
- اردیبهشت 1391 8
- فروردین 1391 13
- اسفند 1390 7
- بهمن 1390 6
- دی 1390 11
- آذر 1390 2
- آبان 1390 6
- مهر 1390 4
- شهریور 1390 5
- مرداد 1390 8
- تیر 1390 15
- خرداد 1390 25
- اردیبهشت 1390 11
- فروردین 1390 1
- اسفند 1389 13
- بهمن 1389 12
- دی 1389 5
- آذر 1389 3
- آبان 1389 6
- مهر 1389 7
- شهریور 1389 6
- خرداد 1389 1
- اردیبهشت 1389 3
- اسفند 1388 7
- بهمن 1388 10
- دی 1388 11
- آذر 1388 7
- آبان 1388 17
- آذر 1387 1
- آبان 1387 9
- مهر 1387 5
- شهریور 1387 1
- مرداد 1387 3
- تیر 1387 7
- خرداد 1387 5
- اردیبهشت 1387 1
- فروردین 1387 3
- اسفند 1386 3
- بهمن 1386 9
- دی 1386 19
- آذر 1386 19
- آبان 1386 7
تقویم
تیر 1404| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
جستجو
پوش یک دسته منحنی و طریقه یافتن آن (2)
برای قسمت اول این مقاله کلیک کنید.
مثال: پوش دسته منحنی زیر را بیابید:
(x-c)2+y2=9
َAdvertisement  |  |
حل - این دسته منحنی معرف دوایری به مرکز نقطه (c,0) و شعاع 3 است. برای بدست آوردن پوش دستگاه زیر را حل می کنیم:
f(x,y)=(x-c)2+y2-9=0
fc(x,y)=2(x-c)=0 -> x=c
در معادله دوم نسبت به c مشتق گرفته شده است. اگر در معادله دایره قرار دهیم x=c خواهیم داشت:
(c-c)2+y2=9->y=3 , y=-3
دو خط افقی مزبور معادلات پوش دسته منحنی هستند.شکل زیر نمودار دسته منحنی و پوش آن را نشان می دهد.
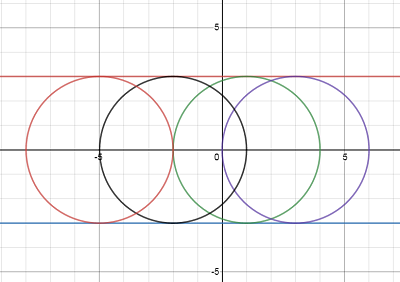
برای ترسیم این نمودار از نرم افزارآانلاین بسیار جالب سایت https://www.desmos.com/calculator استفاده شده است.
پوش یک دسته منحنی و طریقه یافتن آن
دسته ای از منحنی های مسطح که توسط معادله پارامتری زیر مشخص شده را در نظر بگیرید:
f(x,y,C)=0
| که C یک پارامتر است. منظور از پوش (envelope) این دسته منحنی، یک منحنی است که بر تمامی آنها به ازای مقادیر مختلف پارامتر C مماس است. شکل زیر مثالی از یک دسته منحنی پارامتری و پوش آن را نشان می دهد. | Advertisement |
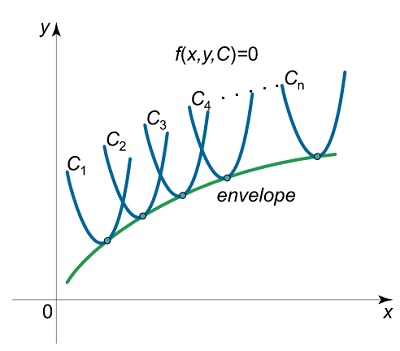
برای بدست آوردن پوش یک دسته منحنی باید دستگاه زیر را حل کرده و پارامتر C را میان آنها حذف کنیم:
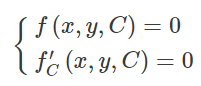
این معادلات شرط لازم برای یافتن پوش یک دسته منحنی را بیان می دارند. ممکن است میان جوابهای این معادلات، نقاطی نیز باشند که در آنها مماس بر منحنی وجود ندارد. برای یافتن شرط کافی وجود پوش، باید نامعادلات زیر همزمان برقرار باشند:
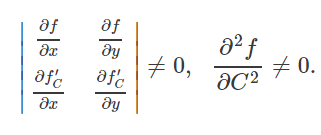
تمام دسته منحنی های پارامتری دارای پوش نیستند. برای مثال دسته دایره هایی که توسط معادله زیر بیان می شوند:
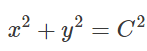
دارای پوش نیستند و این واقعیت از تصویر زیر بخوبی روشن می گردد.
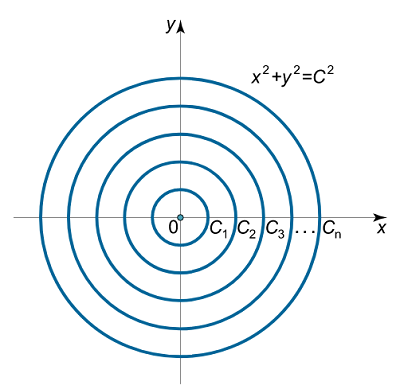
در قسمت دوم این مطلب مثالهایی از پوش دسته منحنی ارائه خواهد شد.