
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبر
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبردرباره من
دستهها
- تصاویر جالب علمی 60
- اخبار علمی 116
- تاریخ علم 21
- مقالات علمی 187
- حقایق علمی 29
- پرسش و پاسخ علمی 4
- تکنولوژی نظامی 170
- مشاهیر 11
- معرفی وبسایت علمی 10
- سخن بزرگان 4
- تفریح و سرگرمی 1
- شگفتیهای طبیعت 6
- مسابقه علمی 6
- زبان انگلیسی 18
- دیرین شناسی 35
- مهندسی مکانیک 56
- دنیای ریاضیات 54
- فایل های قابل دانلود 8
- پزشکی و سلامت 88
- ترین ها 38
- کنکور 1390 14
- نمونه سوال امتحانی و آزمون 20
- معرفی نرم افزار 4
- واژه نامههای تخصصی 1
- آزمایش های ساده و جالب فیزیک 4
- کنکور 13
- تکنولوژی نفت و حفاری 5
- بانک مقالات علمی 3
- آیرودینامیک و پرواز 6
- استانداردهای مهندسی 6
- محیط زیست 39
- باستان شناسی 5
- پروژه درسی و سمینار 5
- برنامه نویسی کامپیوتر 11
- رپرتاژ آگهی 1
ابر برجسب
کووید 19 کرونا ویروس ریاضیات جنگنده هواپیما ستاره زمین لرزه گرمایش جهانی F-35 موشک کنکور بمب افکن سیاهچاله جنگ جهانی دومبرگهها
جدیدترین یادداشتها
همه- کوارک ها: اجزای سازنده ماده
- آموزش زبان برنامه نویسی پایتون با مثال
- سمی ترین حیوانات طبیعت
- کهن ترین مجسمه ساخت انسان
- راه حل اویلر برای مساله بازل
- ژنتیک: چگونه ویژگیهای خود را از نیاکان به ارث میبریم؟
- برنارد ریمان، آفریدگار هندسه نا اقلیدسی
- ابتذال چیست؟ ریشه آن کدام است؟
- اتمها از کجا آمدهاند؟
- پیری: با گذشت عمر چه اتفاقی برای بدن می افتد؟
- مسایل حل شده از معادلات دیفرانسیل
- لئونارد اویلر
- بخشهای مختلف هواپیما و کارکرد آنها
- انسان بر لبه انقراض
- ساخت بزرگترین هواپیمای حامل پهباد توسط چین
بایگانی
- آبان 1404 2
- مهر 1404 3
- شهریور 1404 3
- مرداد 1404 2
- تیر 1404 2
- خرداد 1404 3
- اردیبهشت 1404 1
- فروردین 1404 1
- اسفند 1403 1
- بهمن 1403 2
- دی 1403 1
- آذر 1403 1
- مهر 1403 1
- شهریور 1403 3
- مرداد 1403 1
- تیر 1403 3
- خرداد 1403 4
- اردیبهشت 1403 3
- فروردین 1403 2
- اسفند 1402 7
- بهمن 1402 2
- دی 1402 3
- آذر 1402 3
- آبان 1402 2
- مهر 1402 5
- شهریور 1402 4
- مرداد 1402 12
- تیر 1402 12
- خرداد 1402 5
- اردیبهشت 1402 6
- فروردین 1402 8
- اسفند 1401 6
- بهمن 1401 9
- دی 1401 2
- آذر 1401 3
- آبان 1401 1
- مهر 1401 1
- شهریور 1401 4
- مرداد 1401 7
- تیر 1401 12
- خرداد 1401 10
- اردیبهشت 1401 12
- فروردین 1401 4
- اسفند 1400 4
- بهمن 1400 7
- دی 1400 2
- آبان 1400 5
- مهر 1400 9
- شهریور 1400 1
- مرداد 1400 3
- تیر 1400 6
- خرداد 1400 7
- اردیبهشت 1400 8
- فروردین 1400 7
- اسفند 1399 12
- بهمن 1399 11
- دی 1399 1
- آذر 1399 7
- آبان 1399 2
- مهر 1399 1
- اردیبهشت 1399 7
- فروردین 1399 33
- اسفند 1398 13
- بهمن 1398 9
- دی 1398 1
- خرداد 1398 4
- اردیبهشت 1398 7
- بهمن 1397 5
- دی 1397 5
- آذر 1397 2
- آبان 1397 3
- مهر 1397 3
- شهریور 1397 1
- مرداد 1397 7
- تیر 1397 7
- خرداد 1397 2
- اردیبهشت 1397 6
- اسفند 1396 3
- بهمن 1396 5
- دی 1396 4
- آذر 1396 8
- آبان 1396 6
- مهر 1396 5
- شهریور 1396 6
- مرداد 1396 10
- تیر 1396 9
- خرداد 1396 5
- اردیبهشت 1396 3
- فروردین 1396 8
- اسفند 1395 3
- بهمن 1395 3
- دی 1395 1
- آذر 1395 4
- آبان 1395 2
- مهر 1395 7
- شهریور 1395 5
- مرداد 1395 1
- تیر 1395 3
- خرداد 1395 1
- اردیبهشت 1395 1
- فروردین 1395 3
- اسفند 1394 8
- بهمن 1394 2
- دی 1394 1
- آذر 1394 3
- آبان 1394 2
- مهر 1394 1
- مرداد 1394 1
- تیر 1394 2
- فروردین 1394 1
- اسفند 1393 4
- بهمن 1393 2
- دی 1393 1
- آبان 1393 1
- شهریور 1393 1
- مرداد 1393 1
- تیر 1393 3
- اردیبهشت 1393 7
- فروردین 1393 1
- اسفند 1392 2
- بهمن 1392 8
- دی 1392 6
- آذر 1392 16
- آبان 1392 14
- مهر 1392 19
- شهریور 1392 17
- مرداد 1392 6
- تیر 1392 2
- خرداد 1392 5
- اردیبهشت 1392 9
- فروردین 1392 1
- اسفند 1391 5
- بهمن 1391 8
- دی 1391 6
- آذر 1391 8
- آبان 1391 5
- مهر 1391 12
- شهریور 1391 7
- مرداد 1391 2
- تیر 1391 6
- خرداد 1391 7
- اردیبهشت 1391 8
- فروردین 1391 13
- اسفند 1390 7
- بهمن 1390 6
- دی 1390 11
- آذر 1390 2
- آبان 1390 6
- مهر 1390 4
- شهریور 1390 5
- مرداد 1390 8
- تیر 1390 15
- خرداد 1390 25
- اردیبهشت 1390 11
- فروردین 1390 1
- اسفند 1389 13
- بهمن 1389 12
- دی 1389 5
- آذر 1389 3
- آبان 1389 6
- مهر 1389 7
- شهریور 1389 6
- خرداد 1389 1
- اردیبهشت 1389 3
- اسفند 1388 7
- بهمن 1388 10
- دی 1388 11
- آذر 1388 7
- آبان 1388 17
- آذر 1387 1
- آبان 1387 9
- مهر 1387 5
- شهریور 1387 1
- مرداد 1387 3
- تیر 1387 7
- خرداد 1387 5
- اردیبهشت 1387 1
- فروردین 1387 3
- اسفند 1386 3
- بهمن 1386 9
- دی 1386 19
- آذر 1386 19
- آبان 1386 7
تقویم
آبان 1404| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
جستجو
اعداد شگفت انگیز فیبوناچی
اعداد شگفت انگیز فیبوناچی
میراث امپراتوری روم برای اروپا، سیستم عدد نویسی آن بود که هنوز مورد استفاده قرار میگیرد. اعداد رومی را میتوان در ساعتهای قدیمی و نیز اعلان حق تالیف (copyright) در برنامههای تلویزیونی دید (به عنوا مثال ١٩٩٧ معادل MCMXCVII میباشد.
برای اعداد رومی تا قرن سیزدهم میلادی جایگزینی یافت نشد، تا اینکه فیبوناچی کتاب معروف خود به نام کتاب محاسبات (Liber abaci) را نگاشت.

فیبوناچی که در اصل لئوناردو داپیزا نام داشت، در سال ١١٧٥ میلادی در پیزا به دنیا آمد. او سفرهای زیادی به شمال آفریقا و به بالکان نمود و در سال ١٢٠٠ به پیزا برگشت و دانشی که در طی این سفها آموخته بود را در تالیف کتاب خود بکار گرفت. در این کتاب او سیستم اعشاری عددنویسی را به دنیای لاتین معرفی کرد. اولین فصل بخش نخستین کتاب با این جمله آغاز میشود:
هندیها نه رقم بکار میبرند: ٩ ٨ ٧ ٦ ٥ ٤ ٣ ٢ ١. با این نه رقم و علامت ٠ که در عربی زفیرم خوانده میشود، هر عددی را میتوان نگاشت.
پیدا کردن ریشه معادلات
فیبوناچی قادر به انجام کارهای جالب توجهی در ریاضیات بود. او توانست جواب مثبت معادله زیر را پیدا کند:
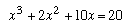
جالب توجهتر آنکه او تمام کارهای ریاپی خود را در سیستم شصتگانی بابلیها انجام میداد. او نتیجه حل این معادله را بصورت زیر بیان کرد:
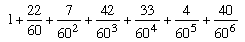
روشی که او در حل این معادله بکار برد نامعلوم است. لیکن او این عمل را سیصد سال پیش از آنکه شخص دیگری قادر به حل معادله شود، انجام داد. جالب اینکه او محاسبه ریشه به سیستم شصتگانی را درست زمانی انجام داد که به دیگران استفاده از سیستم دهدهی را توصیه میکرد!
دنباله فیبوناچی
شاید مشهورترین کار فیبوناچی دنباله عددی معروف او باشد. این دنباله با اعداد ٠ و ١ آغاز میشود. سپس هر عدد از مجموع دو عدد قبلی دنباله بدست میآید. بدین ترتیب دنباله زیر را خواهیم داشت.
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987,...
شاید پرسیده شود که این اعداد از کجا آمدهاند. در روزگار فیبوناچی، مسابقات ریاضی امری معمول بود. در یکی از این مسابقات بود که سوال زیر مطرح شد:
اگر از یک جفت خرگوش شروع کنیم، چنانچه هرماه هر جفت خرگوش بارور، جفت جدیدی بدنیا آورند که آنها نیز پس از یک ماه به باروری رسند، پس از n ماه چند خرگوش خواهیم داشت؟
تصور کنید که پس از n ماه xn جفت خرگوش داشته باشیم. تعداد جفتها در ماه n+1 ، برابر با xn بعلاوه جفتهای جدید بدنیا آمده خواهد بود. اما جفتهای جدید از جفتهایی بدنیا میآیند که حداقل یکماهه باشند. در نتیجه xn-1 جفت جدید خواهیم داشت (تعداد جفتهای جدید بدنیا آمده برابر با جفتهای آماده به تولید مثل است که یکماه پیش بدنیا آمدهاند):
xn+1 = xn + xn-1
و این اساس قاعده تولید اعداد فیبوناچی را تشکیل میدهد.
در قسمت بعد خواص شگفت انگیز این اعداد را بیان خواهیم کرد.
سلام دوست عزیز وبلاگت واقعا جالبه !!!!!به نظر میاد که تو کتاب راز داوینچی را خوندی چون مطالبت کاملا با مطالب کتاب همخونی دارن راستی من در حال تحقیق در مورد جام مقدسم همون جامی که عیسی در شام اخر از ان شراب نوشید اگر در مورد جام مطلبی پیدا کردی لطفا به من میل کن در ضمن در مورد نشان دیر صهیون این نشان نشان اصلی دیر نیست اگه میلت را بدی نشان اصلی را میل میکنم .................... بازم سر می زنم .
سلام بزرگوار
پستهایی که در مورد فیبوناچی گذاشته بودید خوندم
مرسی لذت بردم