دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبر
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبردرباره من
دستهها
- تصاویر جالب علمی 60
- اخبار علمی 116
- تاریخ علم 21
- مقالات علمی 187
- حقایق علمی 29
- پرسش و پاسخ علمی 4
- تکنولوژی نظامی 170
- مشاهیر 11
- معرفی وبسایت علمی 10
- سخن بزرگان 4
- تفریح و سرگرمی 1
- شگفتیهای طبیعت 6
- مسابقه علمی 6
- زبان انگلیسی 18
- دیرین شناسی 35
- مهندسی مکانیک 56
- دنیای ریاضیات 54
- فایل های قابل دانلود 8
- پزشکی و سلامت 88
- ترین ها 38
- کنکور 1390 14
- نمونه سوال امتحانی و آزمون 20
- معرفی نرم افزار 4
- واژه نامههای تخصصی 1
- آزمایش های ساده و جالب فیزیک 4
- کنکور 13
- تکنولوژی نفت و حفاری 5
- بانک مقالات علمی 3
- آیرودینامیک و پرواز 6
- استانداردهای مهندسی 6
- محیط زیست 39
- باستان شناسی 5
- پروژه درسی و سمینار 5
- برنامه نویسی کامپیوتر 11
- رپرتاژ آگهی 1
ابر برجسب
کووید 19 کرونا ویروس ریاضیات جنگنده هواپیما ستاره زمین لرزه گرمایش جهانی F-35 موشک کنکور بمب افکن سیاهچاله جنگ جهانی دومبرگهها
جدیدترین یادداشتها
همه- کوارک ها: اجزای سازنده ماده
- آموزش زبان برنامه نویسی پایتون با مثال
- سمی ترین حیوانات طبیعت
- کهن ترین مجسمه ساخت انسان
- راه حل اویلر برای مساله بازل
- ژنتیک: چگونه ویژگیهای خود را از نیاکان به ارث میبریم؟
- برنارد ریمان، آفریدگار هندسه نا اقلیدسی
- ابتذال چیست؟ ریشه آن کدام است؟
- اتمها از کجا آمدهاند؟
- پیری: با گذشت عمر چه اتفاقی برای بدن می افتد؟
- مسایل حل شده از معادلات دیفرانسیل
- لئونارد اویلر
- بخشهای مختلف هواپیما و کارکرد آنها
- انسان بر لبه انقراض
- ساخت بزرگترین هواپیمای حامل پهباد توسط چین
بایگانی
- آبان 1404 2
- مهر 1404 3
- شهریور 1404 3
- مرداد 1404 2
- تیر 1404 2
- خرداد 1404 3
- اردیبهشت 1404 1
- فروردین 1404 1
- اسفند 1403 1
- بهمن 1403 2
- دی 1403 1
- آذر 1403 1
- مهر 1403 1
- شهریور 1403 3
- مرداد 1403 1
- تیر 1403 3
- خرداد 1403 4
- اردیبهشت 1403 3
- فروردین 1403 2
- اسفند 1402 7
- بهمن 1402 2
- دی 1402 3
- آذر 1402 3
- آبان 1402 2
- مهر 1402 5
- شهریور 1402 4
- مرداد 1402 12
- تیر 1402 12
- خرداد 1402 5
- اردیبهشت 1402 6
- فروردین 1402 8
- اسفند 1401 6
- بهمن 1401 9
- دی 1401 2
- آذر 1401 3
- آبان 1401 1
- مهر 1401 1
- شهریور 1401 4
- مرداد 1401 7
- تیر 1401 12
- خرداد 1401 10
- اردیبهشت 1401 12
- فروردین 1401 4
- اسفند 1400 4
- بهمن 1400 7
- دی 1400 2
- آبان 1400 5
- مهر 1400 9
- شهریور 1400 1
- مرداد 1400 3
- تیر 1400 6
- خرداد 1400 7
- اردیبهشت 1400 8
- فروردین 1400 7
- اسفند 1399 12
- بهمن 1399 11
- دی 1399 1
- آذر 1399 7
- آبان 1399 2
- مهر 1399 1
- اردیبهشت 1399 7
- فروردین 1399 33
- اسفند 1398 13
- بهمن 1398 9
- دی 1398 1
- خرداد 1398 4
- اردیبهشت 1398 7
- بهمن 1397 5
- دی 1397 5
- آذر 1397 2
- آبان 1397 3
- مهر 1397 3
- شهریور 1397 1
- مرداد 1397 7
- تیر 1397 7
- خرداد 1397 2
- اردیبهشت 1397 6
- اسفند 1396 3
- بهمن 1396 5
- دی 1396 4
- آذر 1396 8
- آبان 1396 6
- مهر 1396 5
- شهریور 1396 6
- مرداد 1396 10
- تیر 1396 9
- خرداد 1396 5
- اردیبهشت 1396 3
- فروردین 1396 8
- اسفند 1395 3
- بهمن 1395 3
- دی 1395 1
- آذر 1395 4
- آبان 1395 2
- مهر 1395 7
- شهریور 1395 5
- مرداد 1395 1
- تیر 1395 3
- خرداد 1395 1
- اردیبهشت 1395 1
- فروردین 1395 3
- اسفند 1394 8
- بهمن 1394 2
- دی 1394 1
- آذر 1394 3
- آبان 1394 2
- مهر 1394 1
- مرداد 1394 1
- تیر 1394 2
- فروردین 1394 1
- اسفند 1393 4
- بهمن 1393 2
- دی 1393 1
- آبان 1393 1
- شهریور 1393 1
- مرداد 1393 1
- تیر 1393 3
- اردیبهشت 1393 7
- فروردین 1393 1
- اسفند 1392 2
- بهمن 1392 8
- دی 1392 6
- آذر 1392 16
- آبان 1392 14
- مهر 1392 19
- شهریور 1392 17
- مرداد 1392 6
- تیر 1392 2
- خرداد 1392 5
- اردیبهشت 1392 9
- فروردین 1392 1
- اسفند 1391 5
- بهمن 1391 8
- دی 1391 6
- آذر 1391 8
- آبان 1391 5
- مهر 1391 12
- شهریور 1391 7
- مرداد 1391 2
- تیر 1391 6
- خرداد 1391 7
- اردیبهشت 1391 8
- فروردین 1391 13
- اسفند 1390 7
- بهمن 1390 6
- دی 1390 11
- آذر 1390 2
- آبان 1390 6
- مهر 1390 4
- شهریور 1390 5
- مرداد 1390 8
- تیر 1390 15
- خرداد 1390 25
- اردیبهشت 1390 11
- فروردین 1390 1
- اسفند 1389 13
- بهمن 1389 12
- دی 1389 5
- آذر 1389 3
- آبان 1389 6
- مهر 1389 7
- شهریور 1389 6
- خرداد 1389 1
- اردیبهشت 1389 3
- اسفند 1388 7
- بهمن 1388 10
- دی 1388 11
- آذر 1388 7
- آبان 1388 17
- آذر 1387 1
- آبان 1387 9
- مهر 1387 5
- شهریور 1387 1
- مرداد 1387 3
- تیر 1387 7
- خرداد 1387 5
- اردیبهشت 1387 1
- فروردین 1387 3
- اسفند 1386 3
- بهمن 1386 9
- دی 1386 19
- آذر 1386 19
- آبان 1386 7
تقویم
آبان 1404| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
جستجو
خواص اعجاب انگیز اعداد فیبوناچی
در قسمت قبل، دنباله اعداد فیبوناچی معرفی شدند. در این قسمت برخی از خواص جالب این اعداد بیان میشود.
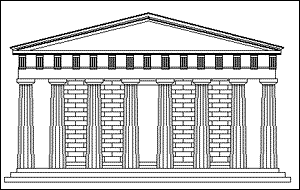
مقدار خاصی که بستگی نزدیکی به دنباله فیبوناچی دارد، نسبت طلایی نامیده میشود. اگر هر عدد در دنباله فیبوناچی را به عدد پیش از خود تقسیم کنیم، مقدار این نسبتها بتدریج به یک عدد ثابت نزدیک میشود. در نمودار شکل زیر این نسبت در مورد هر کدام از اعداد فیبوناچی رسم شده است. همانطور که دیده میشود، این نسبت به یک مقدار حدی نزدیک میشود.
مقدار این نسبت را به سادگی میتوان از یک معادله بدست آورد. شکل زیر طرز محاسبه این نسبت را نشان میدهد. همانطور که میبینید این نسبت معادل 1.618 بدست میآید که یونانیان آنرا با حرف Ф (فی) نشان میدهند.

یونانیان قدیم با این نسبت به خوبی آشنا بودند. معبد معروف پارتنون بهترین مثال از کاربرد این نسبت است. نسبت عرض به طول پنجرههای مستطیل شکل معبد همگی برابر نسبت طلایی است. در اهرام مصر نیز این نسبت بخوبی رعایت شده است. طول هر ضلع قاعده هرکدام از اهرام به ارتفاع آن، معادل نسبت طلایی میباشد.
این نسبت در آناتومی بدن انسان نیز بکار رفته است. اگر قد خود را بر فاصله عمودی ناف تا نوک انگشتان خود تقسیم کنید، تقریبا عدد 1.618 را بدست میآورید. با تقسیم طول بازوی خود از نوک انگشت بزرگ تا بالای شانه، بر فاصله نوک انگشت بزرگ تا آرنج خود نیز به این نسبت میرسید. این نسبت در نقاشی معروف لئوناردو داوینچی به نام مرد ویترووین (Vitruvian Man) که به عنوان لوگوی این وبلاگ انتخاب شده، بدقت شرح داده شده است. از آنجایی که این نسبت در بسیاری از اندازههای بدن انسان وجود دارد، از آن به نام نسبت الهی نیز یاد میشود.
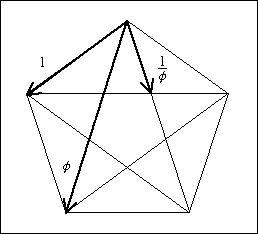
نسبت طلایی حضور خیره کنندهای در هندسه دارد. برای مثال این عدد برابر است با نسبت ضلع یک پنج ضلعی منظم به طول قطر آن. اگر تمام قطرهای یک پنج ضلعی منتظم را بکشیم، یک ستاره پنج پر بدست میآید که علامت بسیاری از پرچمهای دنیاست. این ستاره، به نام ستاره داوود نیز خوانده میشود که نشان دیر صهیون است.


نسبت طلایی در طبیعت نیز بچشم میخورد. تعداد گلبرگهای گلها اغلب برابر با یکی از اعداد فیبوناچی است.تعداد مارپیچهای گل آفتابگردان نیز برابر با یکی از اعداد فیبوناچی است.
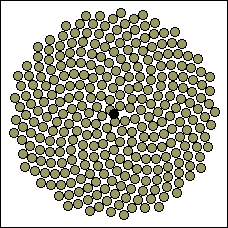

این خواص شگفت انگیز باعث شده است تا برخی، اعداد فیبوناچی را حامل رمزهای پنهان طبیعت بدانند.
منبع اصلی:
اعداد شگفت انگیز فیبوناچی
اعداد شگفت انگیز فیبوناچی
میراث امپراتوری روم برای اروپا، سیستم عدد نویسی آن بود که هنوز مورد استفاده قرار میگیرد. اعداد رومی را میتوان در ساعتهای قدیمی و نیز اعلان حق تالیف (copyright) در برنامههای تلویزیونی دید (به عنوا مثال ١٩٩٧ معادل MCMXCVII میباشد.
برای اعداد رومی تا قرن سیزدهم میلادی جایگزینی یافت نشد، تا اینکه فیبوناچی کتاب معروف خود به نام کتاب محاسبات (Liber abaci) را نگاشت.

فیبوناچی که در اصل لئوناردو داپیزا نام داشت، در سال ١١٧٥ میلادی در پیزا به دنیا آمد. او سفرهای زیادی به شمال آفریقا و به بالکان نمود و در سال ١٢٠٠ به پیزا برگشت و دانشی که در طی این سفها آموخته بود را در تالیف کتاب خود بکار گرفت. در این کتاب او سیستم اعشاری عددنویسی را به دنیای لاتین معرفی کرد. اولین فصل بخش نخستین کتاب با این جمله آغاز میشود:
هندیها نه رقم بکار میبرند: ٩ ٨ ٧ ٦ ٥ ٤ ٣ ٢ ١. با این نه رقم و علامت ٠ که در عربی زفیرم خوانده میشود، هر عددی را میتوان نگاشت.
پیدا کردن ریشه معادلات
فیبوناچی قادر به انجام کارهای جالب توجهی در ریاضیات بود. او توانست جواب مثبت معادله زیر را پیدا کند:
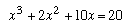
جالب توجهتر آنکه او تمام کارهای ریاپی خود را در سیستم شصتگانی بابلیها انجام میداد. او نتیجه حل این معادله را بصورت زیر بیان کرد:
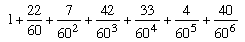
روشی که او در حل این معادله بکار برد نامعلوم است. لیکن او این عمل را سیصد سال پیش از آنکه شخص دیگری قادر به حل معادله شود، انجام داد. جالب اینکه او محاسبه ریشه به سیستم شصتگانی را درست زمانی انجام داد که به دیگران استفاده از سیستم دهدهی را توصیه میکرد!
دنباله فیبوناچی
شاید مشهورترین کار فیبوناچی دنباله عددی معروف او باشد. این دنباله با اعداد ٠ و ١ آغاز میشود. سپس هر عدد از مجموع دو عدد قبلی دنباله بدست میآید. بدین ترتیب دنباله زیر را خواهیم داشت.
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987,...
شاید پرسیده شود که این اعداد از کجا آمدهاند. در روزگار فیبوناچی، مسابقات ریاضی امری معمول بود. در یکی از این مسابقات بود که سوال زیر مطرح شد:
اگر از یک جفت خرگوش شروع کنیم، چنانچه هرماه هر جفت خرگوش بارور، جفت جدیدی بدنیا آورند که آنها نیز پس از یک ماه به باروری رسند، پس از n ماه چند خرگوش خواهیم داشت؟
تصور کنید که پس از n ماه xn جفت خرگوش داشته باشیم. تعداد جفتها در ماه n+1 ، برابر با xn بعلاوه جفتهای جدید بدنیا آمده خواهد بود. اما جفتهای جدید از جفتهایی بدنیا میآیند که حداقل یکماهه باشند. در نتیجه xn-1 جفت جدید خواهیم داشت (تعداد جفتهای جدید بدنیا آمده برابر با جفتهای آماده به تولید مثل است که یکماه پیش بدنیا آمدهاند):
xn+1 = xn + xn-1
و این اساس قاعده تولید اعداد فیبوناچی را تشکیل میدهد.
در قسمت بعد خواص شگفت انگیز این اعداد را بیان خواهیم کرد.
سخن بزرگان (١)
It has become appallingly obvious that our technology has exceeded our humanity.
اکنون بطرز خوفناکی آشکار شده که فناوری ما بر انسانیت ما پیشی گرفته است. (آلبرت اینشتین ١٨٧٩-١٩٥٥)
Imagination is more important than knowledge, for the knowledge is limited, but imagination encircles the entire world.
تخیل مهمتر از دانش است، زیرا دانش بشری محدود است، لیکن تخیل تمامی مرزهای عالم را در می نوردد. (آلبرت اینشتین ١٨٧٩-١٩٥٥)
As far as the laws of mathematics refer to reality, they are not certain, and as far as they are certain, they do not refer to reality.
قوانین ریاضیات تا زمانی معرف واقعیت هستند که از عدم قطعیت برخوردار باشند. زمانیکه این قوانین دارای قطعیت باشند، دیگر معرف واقعیت نیستند. (آلبرت اینشتین ١٨٧٩-١٩٥٥)
Knowledge is power.
(Ipsa Scientia Potestas Est)
دانش، قدرت است (سر فرانسیس بیکن ١٥٦١-١٦٢٦)
Discretion in speech is more than eloquence.
حزم و احتیاط در سخن گفتن، برتر از سخنوری و فصاحت کلام است (سر فرانسیس بیکن ١٥٦١-١٦٢٦)
The saddest aspect of life right now is that science gathers knowledge faster than society gathers wisdom.
اندوهبارترین جنبه زندگی این است که دانشی که توسط علوم تولید می شود، آهنگ رشدی بسیار سریعتر از کسب خرد توسط جامعه دارد (خرد جمعی در جامعه انسانی بسیار عقب تر از علوم نوین حرکت می کند).
(آیزاک آسیموف ١٩٢٠-١٩٩٢)
روبوت های نظامی (قسمت دوم)
تالون
تالون یک روبوت قابل حمل است که بر روی زنجیرهای کوچک حرکت می کند. وزن آن معمولا کمتر از ٤٥ کیلوگرم است. تالون بسیار بادوام است. بنا بر گزارش ها یکی از این روبوتها از بالای پلی در عراق به داخل رودخانه سقوط کرد. لیکن مدتی بعد سربازان با استفاده از واحد کنترل از راه دور توانستند انرا از داخل رودخانه به بیرون هدایت کنند. این امر موجب کشف ویژگی مهم دیگری برای این روبوت شد: خاصیت دوزیستی آن.
تالون با استفاده از جوی استیک هدایت می شود و دارای هفت تنظیم سرعت است. می تواند با استفاده از زنجیرهای خود از پلکان بالا رفته و روی زمینهای صخرهای مانور کرده و حتی روی برف حرکت کند.
تالون می تواند به اشکال مختلفی پیکربندی شده و متناسب با موقعیت تغییر شکل داده شود. استفاده اصلی آن در خنثی سازی مینها و بمب های عمل نکرده است.
اخیرا نمونههایی از این روبوت به حسگرهای شیمیایی، گاز، دما و تشعشعات مجهز شده است. ارتش آمریکا حتی در حال مسلح کردن برخی انواع این روبوت به سلاح های خودکار است. حتی برخی انواع این روبوتها قرار است به نارنجک انداز و پرتاب کننده راکت ضدتانک مجهز شوند.

روبوت های نظامی
هرکسی می داند که سربازی شغل خطرناکی است. اما برخی از وظایفی که سربازان باید انجام دهند، بسیار خطرناکتر از بقیه می باشد. عبور از میدان مین، خنثی کردن بمب های منفجر نشده و پاکسازی ساختمانهای بجای مانده از دشمن از خطرناکترین وظایفی است که ممکن است بر عهده سربازان گذارده شود.
اگر بتوان برخی از این وظایف را بر عهده روبوتها گذاشت، جان سربازان حفظ می شود و در صورت بروز اشتباه، تنها پول و امکانات مادی از دست می رود.
ارتش آمریکا سالهاست که روبوتهای نظامی را برای انجام کارهای مختلفی ساخته است و چند نمونه از آنها هم اکنون در جبهه عراق مورد استفاده واقع شده اند. در این مقاله نگاهی به روبوتهای نظامی و آینده توسعه و تکامل آنها خواهیم انداخت.
منبع:
How Military Robots Work
http://science.howstuffworks.com/military-robot.htm
روبوتهای نظامی با آن ماشینهای انسان نمایی که در فیلمهایی مانند ترمیناتور می بینیم، تفاوت زیادی دارند. روبوتها دارای اندازه و اشکال متفاوتی می باشند. تعریف ساده ای که می توان برای روبوت ارائه کرد بدین صورت است: ماشینی که بخشی یا تمام آن توسط یک کامپیوتر سرخود (Onboard) کنترل می شود. روبوتها دارای حسگرهایی نیز هستند که به آنها امکان می دهد از محیط اطراف خود اطلاعات جمع آوری کنند. همچنین به وسیلهای برای حرکت و یک منبع نیرو نیز مجهز هستند.

یک روبوت برای پاکسازی میادین مین
شکل روبوتهای نظامی به کاری که انجام می دهند بستگی دارد. روبوتهایی که باید در زمینهای دشوار حرکت کنند، از زنجیرچرخهایی مانند تانک استفاده می کنند.روبوتهای پرنده کاملا شبیه هواپیماهای کوچک هستند. برخی از روبوتها نیز شباهت زیادی به کامیونها و بولدوزرها دارند.
روبوتهای نظامی امروزه خود به تنهایی قادر به انجام کار زیادی نیستند. مغز کامپیوتری آنها از نظر هوش مصنوعی (Artificial Intelligence) چندان پیشرفته بشمار نمی رود. یعنی قادر به پردازش پیچیده اطلاعات و تصمیم گیری بر اساس آنها نیستند. بجای استفاده از هوش مصنوعی مستقل،بیشتر روبوتهای نظامی از راه دور توسط اپراتورهای انسانی هدایت می شوند. ارتش معمولا از واژه روبوت برای این ماشین ها استفاده نمی کند، بلکه آنها را با نام خودروهای زمینی بدون سرنشین (unmanned ground vehicles=UGV) یا خودروهای هوایی بدون سرنشین (unmanned aerial vehicles=UAV) می نامد.
پایان قسمت اول