
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبر
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبردرباره من
دستهها
- تصاویر جالب علمی 60
- اخبار علمی 116
- تاریخ علم 21
- مقالات علمی 187
- حقایق علمی 29
- پرسش و پاسخ علمی 4
- تکنولوژی نظامی 170
- مشاهیر 11
- معرفی وبسایت علمی 10
- سخن بزرگان 4
- تفریح و سرگرمی 1
- شگفتیهای طبیعت 6
- مسابقه علمی 6
- زبان انگلیسی 18
- دیرین شناسی 35
- مهندسی مکانیک 56
- دنیای ریاضیات 54
- فایل های قابل دانلود 8
- پزشکی و سلامت 88
- ترین ها 38
- کنکور 1390 14
- نمونه سوال امتحانی و آزمون 20
- معرفی نرم افزار 4
- واژه نامههای تخصصی 1
- آزمایش های ساده و جالب فیزیک 4
- کنکور 13
- تکنولوژی نفت و حفاری 5
- بانک مقالات علمی 3
- آیرودینامیک و پرواز 6
- استانداردهای مهندسی 6
- محیط زیست 39
- باستان شناسی 5
- پروژه درسی و سمینار 5
- برنامه نویسی کامپیوتر 11
- رپرتاژ آگهی 1
ابر برجسب
کووید 19 کرونا ویروس ریاضیات جنگنده هواپیما ستاره زمین لرزه گرمایش جهانی F-35 موشک کنکور بمب افکن سیاهچاله جنگ جهانی دومبرگهها
جدیدترین یادداشتها
همه- کوارک ها: اجزای سازنده ماده
- آموزش زبان برنامه نویسی پایتون با مثال
- سمی ترین حیوانات طبیعت
- کهن ترین مجسمه ساخت انسان
- راه حل اویلر برای مساله بازل
- ژنتیک: چگونه ویژگیهای خود را از نیاکان به ارث میبریم؟
- برنارد ریمان، آفریدگار هندسه نا اقلیدسی
- ابتذال چیست؟ ریشه آن کدام است؟
- اتمها از کجا آمدهاند؟
- پیری: با گذشت عمر چه اتفاقی برای بدن می افتد؟
- مسایل حل شده از معادلات دیفرانسیل
- لئونارد اویلر
- بخشهای مختلف هواپیما و کارکرد آنها
- انسان بر لبه انقراض
- ساخت بزرگترین هواپیمای حامل پهباد توسط چین
بایگانی
- آبان 1404 2
- مهر 1404 3
- شهریور 1404 3
- مرداد 1404 2
- تیر 1404 2
- خرداد 1404 3
- اردیبهشت 1404 1
- فروردین 1404 1
- اسفند 1403 1
- بهمن 1403 2
- دی 1403 1
- آذر 1403 1
- مهر 1403 1
- شهریور 1403 3
- مرداد 1403 1
- تیر 1403 3
- خرداد 1403 4
- اردیبهشت 1403 3
- فروردین 1403 2
- اسفند 1402 7
- بهمن 1402 2
- دی 1402 3
- آذر 1402 3
- آبان 1402 2
- مهر 1402 5
- شهریور 1402 4
- مرداد 1402 12
- تیر 1402 12
- خرداد 1402 5
- اردیبهشت 1402 6
- فروردین 1402 8
- اسفند 1401 6
- بهمن 1401 9
- دی 1401 2
- آذر 1401 3
- آبان 1401 1
- مهر 1401 1
- شهریور 1401 4
- مرداد 1401 7
- تیر 1401 12
- خرداد 1401 10
- اردیبهشت 1401 12
- فروردین 1401 4
- اسفند 1400 4
- بهمن 1400 7
- دی 1400 2
- آبان 1400 5
- مهر 1400 9
- شهریور 1400 1
- مرداد 1400 3
- تیر 1400 6
- خرداد 1400 7
- اردیبهشت 1400 8
- فروردین 1400 7
- اسفند 1399 12
- بهمن 1399 11
- دی 1399 1
- آذر 1399 7
- آبان 1399 2
- مهر 1399 1
- اردیبهشت 1399 7
- فروردین 1399 33
- اسفند 1398 13
- بهمن 1398 9
- دی 1398 1
- خرداد 1398 4
- اردیبهشت 1398 7
- بهمن 1397 5
- دی 1397 5
- آذر 1397 2
- آبان 1397 3
- مهر 1397 3
- شهریور 1397 1
- مرداد 1397 7
- تیر 1397 7
- خرداد 1397 2
- اردیبهشت 1397 6
- اسفند 1396 3
- بهمن 1396 5
- دی 1396 4
- آذر 1396 8
- آبان 1396 6
- مهر 1396 5
- شهریور 1396 6
- مرداد 1396 10
- تیر 1396 9
- خرداد 1396 5
- اردیبهشت 1396 3
- فروردین 1396 8
- اسفند 1395 3
- بهمن 1395 3
- دی 1395 1
- آذر 1395 4
- آبان 1395 2
- مهر 1395 7
- شهریور 1395 5
- مرداد 1395 1
- تیر 1395 3
- خرداد 1395 1
- اردیبهشت 1395 1
- فروردین 1395 3
- اسفند 1394 8
- بهمن 1394 2
- دی 1394 1
- آذر 1394 3
- آبان 1394 2
- مهر 1394 1
- مرداد 1394 1
- تیر 1394 2
- فروردین 1394 1
- اسفند 1393 4
- بهمن 1393 2
- دی 1393 1
- آبان 1393 1
- شهریور 1393 1
- مرداد 1393 1
- تیر 1393 3
- اردیبهشت 1393 7
- فروردین 1393 1
- اسفند 1392 2
- بهمن 1392 8
- دی 1392 6
- آذر 1392 16
- آبان 1392 14
- مهر 1392 19
- شهریور 1392 17
- مرداد 1392 6
- تیر 1392 2
- خرداد 1392 5
- اردیبهشت 1392 9
- فروردین 1392 1
- اسفند 1391 5
- بهمن 1391 8
- دی 1391 6
- آذر 1391 8
- آبان 1391 5
- مهر 1391 12
- شهریور 1391 7
- مرداد 1391 2
- تیر 1391 6
- خرداد 1391 7
- اردیبهشت 1391 8
- فروردین 1391 13
- اسفند 1390 7
- بهمن 1390 6
- دی 1390 11
- آذر 1390 2
- آبان 1390 6
- مهر 1390 4
- شهریور 1390 5
- مرداد 1390 8
- تیر 1390 15
- خرداد 1390 25
- اردیبهشت 1390 11
- فروردین 1390 1
- اسفند 1389 13
- بهمن 1389 12
- دی 1389 5
- آذر 1389 3
- آبان 1389 6
- مهر 1389 7
- شهریور 1389 6
- خرداد 1389 1
- اردیبهشت 1389 3
- اسفند 1388 7
- بهمن 1388 10
- دی 1388 11
- آذر 1388 7
- آبان 1388 17
- آذر 1387 1
- آبان 1387 9
- مهر 1387 5
- شهریور 1387 1
- مرداد 1387 3
- تیر 1387 7
- خرداد 1387 5
- اردیبهشت 1387 1
- فروردین 1387 3
- اسفند 1386 3
- بهمن 1386 9
- دی 1386 19
- آذر 1386 19
- آبان 1386 7
تقویم
آبان 1404| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
جستجو
موتورهای جستجوی وب چگونه کار میکنند؟
منبع اصلی: Webopedia
ترجمه: اصغر ناصری - زمستان 1391
موتورهای جستجو ابزار اصلی یافتن اطلاعات در پهنه عظیم وب جهان گستر هستند. بدون موتورهای جستجوی پیشرفته، یافتن اطلاعات مورد نظر در اینترنت تقریبا غیرممکن خواهد بود مگر این که آدرس URL صفحه وب مورد نظر را دقیقا بدانید. در این مقاله نگاه کوتاهی خواهیم انداخت به نحوه کار کردن موتورهای جستجو و عواملی که برخی از آنها را در صدر توجه کاربران قرار میدهد.
وقتی افراد از واژه موتور جستجوی وب استفاده می کنند معمولا منظورشان فرم های جستجویی است که امکان جستجو در میان اسناد HTML گردآوری شده توسط برنامه ای به نام روبوت را میدهند.
اساسا سه نوع موتور جستجو وجود دارد: آنهایی که توسط روبوت عمل گردآوری اطلاعات را انجام می دهند و به نام خزنده (crawler)، مورچه (ant) یا عنکبوت (spider) خوانده می شوند (زیرا عملی مانند خزیدن در پهنه عظیم وب و گردآوری تدریجی داده را انجام می دهند) و آنهایی که اطلاعات آنها توسط افراد گردآوری می شود و بالاخره موتورهای جستجویی که ترکیبی از هر دو عمل را انجام می دهند.
موتورهای جستجوی مبتنی بر روبوت از نرمافزارهای خودکار استفاده می کنند. این نرمافزارها یک وب سایت را بازدید کرده، اطلاعات موجود در صفحات آن را خوانده و متا تگ های سایت را بررسی میکنند. همچنین لینکهای موجود در هر صفحه را نیز شناسایی میکنند تا صفحاتی که لینک ها به آنها متصل میشوند را نیز بدین ترتیب مورد بازدید و نمایهسازی قرار دهند. روبوت تمامی اطلاعات گردآوری شده را به مخزن داده مرکزی میفرستد تا در آنجا اطلاعات نمایهسازی شود. منظور از نمایهسازی ذخیره کلید واژههای اصلی همراه با آدرسی است که این کلید واژهها در آنجا مشاهده شدهاند. روبوت بطور دورهای وب سایتهای قبلی را بازدید میکند تا تغییر اطلاعات موجود در آنها را ثبت کند.
موتورهای جستجویی که توسط انسانها تغذیه می شوند تنها اطلاعاتی را گردآوری و نمایه میکنند که توسط عوامل انسانی به آنها ارسال شده است.
در هرحال، وفتی عبارتی را در موتور جستجو می کاوید، در حقیقت نمایه ای را جستجو می کنید که موتور جستجو از پیش آماده و ذخیره کرده است. بنابراین واقعا وب را جستجو نمی کنید. این نمایهها بانک های اطلاعاتی غول آسایی از تریلیون ها آدرس می توانند باشند. به همین دلیل برخی نتایجی که موتورهای جستجوی بزرگی مانند Yahoo یا Google بر میگردانند لینک های غیرمعتبر یا مرده هستند. از آنجایی که نتایج جستجوی مبتنی بر نمایه هستند، اگر نمایه مرتب بروز نشود ممکن است حاوی اطلاعاتی مربوط به صفحاتی باشد که دیگر در وب موجود نیستند.
موتورهای جستجوی مختلف از الگوریتم های اختصاصی خود برای رتبه بندی نتایج استفاده میکنند. به همین دلیل برخی موتورهای جستجو بهتر و سریع تر شما را به نتیجه مورد نظر میرسانند.
یکی از عناصر اصلی مورد پویش الگوریتم های جستجو، تعداد و مکان ظهور کلیدواژه ها در یک صفحه وب است. هرچه تکرار کلیدواژه ای در یک صقحه وب بیشتر باشد، موتور جستجو اهمیت بیشتری برای آن صفحه قایل شده و آن را در نتایج جستجو در رده بالاتری قرار می دهد. البته الگوریتم های مورد استفاده موتورهای جستجو روز بروز حرفه ای تر می شوند تا صفخات قلابی با محتوای بی ارزش را تشخیص دهند.
نگاهی به تاریخ موتورهای جستجو
اولین ابزار جستجوی اینترنت در سال 1990 ابداع شد که Archie نام داشت. این ابزار فهرست های سبسبه مراتبی از تمام فایل هایی که روی سرورهای بدون نام FTP بودند تولید می کرد و بدین ترتیب یک بانک اطلاعاتی قابل جستجو از نام فایل ها ایجاد مینمود.یکسال بعد Gopher پا به عرصه گذاشت که می توانست اسناد ایجاد شده با متن ساده را شناسایی و نمایه کند. ورونیکا و جاگ هد دو ابزار فرعی برای جستجوی سیستم نمایه گوفر بودند. اولین موتور جستجوی واقعی وب توسط ماتیو گری در 1993 ابداع شد و Wandex نام داشت.
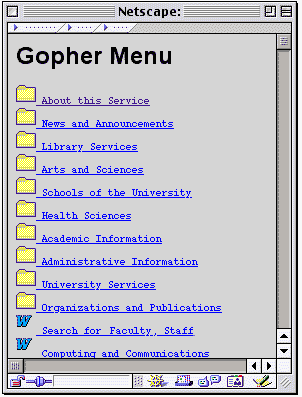
نمونه ای از فهرست های Gopher
در مارس 1996 دو دانشجوی دانشگاه استانفورد به نام های لری پیج و سرگئی برین پروژه ای تحقیقاتی به نام موتور جستجوی گوگل را آغاز کردند. این پروژه تحقیقاتی دانشگاهی بتدریج به یکی از بزرگترین و موفق ترین موتورهای جستجوی وب تبدیل شد و هم اکنون کمپانی گوگل در زمره بزرگترین شرکت های دنیای کامپیوتر و اینترنت محسوب می شود. تصویر زیر صفحه موتور جستجوی گوگل در سال 1998 را نشان می دهد:
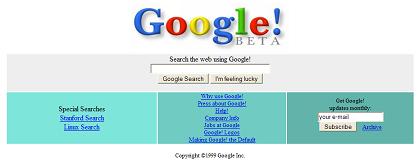
برای اطلاعات بیشتر به این مقاله مراجعه کنید:
صحنههای برجستهای از نمایشگاه لوازم الکترونیک 2013
عکس های زیر از نمایشگاه لوازم الکترونیک 2013 (International Consumer Electronics Show) انتخاب شده است.
منبع: سایت Yahoo News

رپتار (Reptar) یک مار رباتیک است که توسط شرکت Lego در نمایشگاه CES معرفی خواهد شد. این ربات قادر به مکالمه با iPhone، iPad و iPod از طریق بلوتوث خواهد بود.

لنز الکترونیکی سامسونگ که با فشردن یک سوئیچ میتواند از حالت دو بعدی به تصویربرداری سه بعدی منتقل شود.

مدل Sharp IGZO Tablet Aquos Pad که از فناوری نوین شرکت شارپ تحت عنوان IGZO استفاده میکند. فناوری IGZO (اکسید روی گالیوم ایندیوم) کیفیت تصویر بسیار بالا با توان مصرفی اندک ایجاد می کند.

دوربین ویدیویی کیفیت بالای EGO که مجهز به فناوری WiFi است و می تواند از طریق امواج شبکه تلفن همراه اطلاعات ارسال کند. قیمت خرده فروشی این دوربین 179 دلار است.

ماوسی با 12 تکمه ساخت شرکت Genius. این ماوس بسیار دقیق مناسب بازی های رایانهای است.
الگوهای جالب اعداد
به چند الگوی جالب اعداد که در زیر معرفی شده توجه کنید. آیا میتوانید توضیحی برای آنها بیابید؟
الگوی اول:
12345679 x 9 = 111,111,111
12345679 x 18 = 222,222,222
12345679 x 27 = 333,333,333
12345679 x 36 = 444,444,444
12345679 x 45 = 555,555,555
12345679 x 54 = 666,666,666
12345679 x 63 = 777,777,777
12345679 x 72 = 888,888,888
12345679 x 81 = 999,999,999
دقت کنید که عامل های دوم ضرب، مضارب عدد نه هستند و رقم 8 از دنباله ارقام 12345679 غایب است.
الگوی دوم:
1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
الگوی سوم:
0 x 9 + 1 = 1
1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
الگوی چهارم:
0 x 9 + 8 = 8
9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
هواپیماهای شگفت انگیز: بمب افکن بی 17
تالیف: اصغر ناصری
پس از پایان جنگ جهانی اول اهمیت نیروی هوایی بر همگان معلوم گشت. ویران شدن شهر گوئرنیکا در جریان جنگ داخلی اسپانیا توسط لژیون کندورهای آلمانی اهمیت بمب افکن ها را بر تمامی صاحب نظران نظامی دنیا آشکار ساخت.
در 8 آگوست سال 1934 سپاه هوایی ارتش آمریکا (که بعدها با استقلال از نیروی زمینی به نیروی هوای آمریکا تبدیل شد) مناقصهای را برای تامین یک بمب افکن که قادر به پرواز با سرعت 400 کیلومتر بر ساعت، برد 3200 کیلومتر و سقف پرواز عملیاتی 3000 متر باشد صادر کرد. کمپانی بوئینگ تقریبا تمامی سرمایه ذخیره و نیروی انسانی خود را برای تکمیل این کار بعهده گرفت و نمونه ای به نام مدل 2-99 ارائه کرد.
در جولای 1935 مدل 2-99 بوئینگ که بمب افکنی تمام فلزی با چهار موتور و 15 تن وزن بود اولین پرواز خود را انجام داد. توانایی فنی هواپیما بیشتر از اعلام نیاز ارتش بود. یک گزارشگر این بمب افکن جدید را بخاطر تعداد زیاد مسلسل های دفاعی آن دژ پرنده (Flying Fortress) نام گذاری کرد. این نام همچنان بر این بمب افکن باقی ماند.

لیکن این بمب افکن رقابت را به داگلاس DB1 باخت. با این وجود تعداد کمی از این هواپیماها برای ارزیابی بیشتر به بوئینگ سفارش داده شد.
با وخامت اوضاع در اروپا، ثابت شد بمب افکن داگلاس DB1 از توان کافی برخوردار نیست. تا آن زمان بوئینگ مدل 2-99 را به YB-17 ارتقا داده بود که دارای موتورهای سوپرشارژ و سقف پروازی حدود 9100 متر بود. در ابتدای جنگ جهانی دوم دارای 30 فروند بی 17 بود.
در سال 1941 آمریکا 20 عدد از این بمب افکن ها را برای کمک به انگلستان به بریتانیا فرستاد. آنها شروعی شوم داشتند. اولین بمب افکن ارسالی سقوط کرد و دوتا از آنها که برای حمله به پایگاه دریایی ویلهلم شاون فرستاده شده بودند ماموریتی ناموفق داشتند.
حمله ژاپنی ها به پرل هاربر آمریکا را وارد جنگ جهانی دوم کرد و به کمپانی بوئینگ دستور داده شد هرچه در توان دارد برای تولید بی 17 بکار گیرد.
در این زمان نیروی هوایی هشتم آمریکا در بریتانیا مستقر شده بود. بریتانیایی ها تصمیم به بمباران شبانه خاک آلمان گرفتند تا امنیت هواپیماها را تامین کنند اما آمریکایی ها معتقد بودند بمباران روزانه به علت دقت آن موثرتر و کم هزینه تر است.
اولین ماموریت مهم بی 17 ها علیه آلمان در آگوست 1942 انجام شد. بی 17 ها در یک آرایش گوه شکل پرواز می کردند تا بتوانند از آتش حجیم مسلسل های خود علیه جنگنده های مهاجم آلمان استفاده کنند. لیکن خلبانان آلمانی بزودی دریافتند حمله از روبرو علیه آرایش بی 17 ها موثرتر است زیرا مسلسل های این بمب افکن ها بیشتر در پهلوهای آنها مستقر بود.

در ژانویه 1943 روزولت و چرچیل دستورالعمل کازابلانکا را صادر کردند که تصمیم بر بمباران صنایع کلیدی آلمان را محور کار قرار داده بود.
در 17 آگوست 1943 آرایشی از 211 بمب افکن بی 17 به کارخانه بلبرینگ شواین فورت آلمان حمله کردند. این حمله بسیار مهم بود زیرا 2 درصد تمامی بلبرینگ های آلمان در این مجتمع تولید می شد. در طی این حمله 60 بی 17 نابود شدند. در 1943 پیش بینی می شد که یک سوم بی 17 ها نتوانند پس از حمله جان سالم بدر برند و این آمار تلفات بالا باعث شد حملات روزانه متوقف شود. مدل B-17G به یک توپ دماغه ای مجهز بود تا قدرت آتش از جلو را فراهم کند و این امر تلفات این هواپیما را کاهش داد. اما ظهور جنگنده اسکورت پی 51 موستانگ که بسیار چابک و پرقدرت بود حمایت موثری برای این بمب افکن ها در 1944 فراهم کرد بطوری که تلفات آنها بسیار کاهش یافت.
در فوریه 1944 بی 17 ها تمامی کارخانجات حساس آلمان را بمباران کردند. در کل 3500 بمبافکن بی 17 در بمباران کارخانجات آلمانی بکار رفتند که 244 عدد معادل 7 درصد آنها تنها در یک هفته ساقط شدند. لیکن توانستند کمر صنایع آلمان را خرد کنند. از آن پس آلمان به تعداد کافی قطعات یدکی برای پرواز هواپیماهای خود نداشت. تا انتهای جنگ بی 17 ها 70 درصد برلین را با خاک یکسان کرده بودند. صنایع نفت آلمان هدف حساس دیگر بود و نابودی آنها که به قیمت 922 بی 17 تمام شد کار آلمان نازی را یکسره کرد. در پایان جنگگ جهانی دوم تنها 300 تانک تایگر آلمان به علت نداشتن سوخت در ایستگاه قطار زمین گیر شده و قادر به اعزام به جبهههای جنگ نبودند.
بی 17 های نیروی هوایی هشتم آمریکا و نیروی هوای سلطنتی انگلستان در طول یورش های خود به آلمان حدود پانصد هزار تن بمب بر سر شهرهای مختلف این کشور ریختند. بیش از 99 میلیون گلوله از مسلسل های این بمب افکن ها شلیک شد و این باور وجود دارد که 20 هزار هواپیمای آلمانی توسط این بمب افکن ها در هوا و بر روی زمین نابود شدند. حدود 12 هزار بی 17 توسط کمپانی بوئینگ ساخته شد و 250 هزار آمریکایی تجربه پرواز با این هواپیما را کسب کردند. که 46 هزار و پانصد تن از آنها کشته یا زخمی شدند. سهم بی 17 ها در عرصه نبرد اروپا بسیار مهم بود.
منبع اصلی:
http://www.historylearningsite.co.uk/b17_flying_fortress.htm
برخی تصاویر جالب:

قطار بی پایانی از بی 17 ها آماده برای پرواز بسوی آلمان

بالاتر از دلهره - عدم نشانه روی صحیح باعث شده بمب رهاشده از هواپیمای بالایی روی بی 17 زیرین سقوط کند
آخرین قضیه فرما
پیر فرما (تولد 1601) بنیان گذار نظریه نوین اعداد محسوب می شود. سالهایی از دهه 1630 زندگی او وقف تصحیح کتاب آریثماتیکا اثر کلاسیک دیوفانتوس شده بود. او در حاشیه این کتاب مطلبی یادداشت کرد که به مدت چهارصدسال ریاضی دانان پس از خود را به تکاپو واداشت.
این مطلب پیرامون قضیه ای بود که اکنون به عنوان آخرین قضیه فرما شناخته می شود. مطابق این قضیه معادله دیوفانتین یعنی 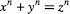 برای n > 2 در مجموعه اعداد صحیح جواب ندارد. به عنوان مثال هیچ سه عدد صحیح مخالف صفر را نمیتوان یافت که معادله x3 + y3 = z3 را برآورده سازد.
برای n > 2 در مجموعه اعداد صحیح جواب ندارد. به عنوان مثال هیچ سه عدد صحیح مخالف صفر را نمیتوان یافت که معادله x3 + y3 = z3 را برآورده سازد.
توجه کنید که برای n=2 معادله به فرم x2+y2 = z2 در میآید که همان قضیه فیثاغورث است و می دانیم بیشمار سه تایی صحیح میتوان پیدا کرد که در معادله فوق صدق کنند.
فرما در حاشیه کتاب ادعا کرد که اثبات این قضیه را یافته است. لیکن از ذکر آن خودداری کرد. اکنون تقریبا مطمئنیم که ادعای فرما خیلی دقیق نبوده و احتمالا برای n=3 و n=4 این قضیه را ثابت کرده، لیکن حل عمومی آن را نیافته است.
در سال 1993 انفجاری در عالم ریاضیات اتفاق افتاد. اندرو وایلز با اثبات حالت نیمه پایدار حدس تانی یاما-شیمورا قضیه فرما را بطور پارهای اثبات کرد. متاسفانه رخنههای متعددی در روش اثبات اندرو وایلز پدیدار شد. لیکن در سال 1994 وایلز و تایلور با همکاری هم مسئله را به یک فرمول شماره رده (Class Number Forula) فرو کاسته و اثبات نهایی آخرین قضیه فرما را ارائه کردند.
اثبات قضیه فرما پایان یک دوران در ریاضیات بود. از آن جایی که ابزارهای مورد استفاده در حل این مسئله هنوز در زمان فرما ابداع نشده بودند، بنظر می رسد حل ادعایی فرما واقعیت نداشته باشد.
در یکی از اپیزودهای کارتون معروف The Simpsons، معادله 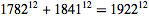 در نقطه ای از پس زمینه تصویر دیده می شود. ممکن است بنظر برسد که این اعداد به ازای n=12 در قضیه فرما صدق میکنند، در حالی که حاصل دو طرف تنها در نه رقم اول با یکدیگر تطابق دارد.
در نقطه ای از پس زمینه تصویر دیده می شود. ممکن است بنظر برسد که این اعداد به ازای n=12 در قضیه فرما صدق میکنند، در حالی که حاصل دو طرف تنها در نه رقم اول با یکدیگر تطابق دارد.

منابعی برای مطالعه بیشتر:
http://mathworld.wolfram.com/FermatsLastTheorem.html