
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبر
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبردرباره من
دستهها
- تصاویر جالب علمی 60
- اخبار علمی 115
- تاریخ علم 21
- مقالات علمی 183
- حقایق علمی 29
- پرسش و پاسخ علمی 4
- تکنولوژی نظامی 170
- مشاهیر 10
- معرفی وبسایت علمی 10
- سخن بزرگان 4
- تفریح و سرگرمی 1
- شگفتیهای طبیعت 6
- مسابقه علمی 6
- زبان انگلیسی 18
- دیرین شناسی 34
- مهندسی مکانیک 56
- دنیای ریاضیات 51
- فایل های قابل دانلود 8
- پزشکی و سلامت 88
- ترین ها 36
- کنکور 1390 14
- نمونه سوال امتحانی و آزمون 20
- معرفی نرم افزار 4
- واژه نامههای تخصصی 1
- آزمایش های ساده و جالب فیزیک 4
- کنکور 13
- تکنولوژی نفت و حفاری 5
- بانک مقالات علمی 3
- آیرودینامیک و پرواز 6
- استانداردهای مهندسی 6
- محیط زیست 38
- باستان شناسی 5
- پروژه درسی و سمینار 5
- برنامه نویسی کامپیوتر 10
- رپرتاژ آگهی 1
ابر برجسب
جنگنده هواپیما ریاضیات ستاره زمین لرزه گرمایش جهانی F-35 سیاهچاله جنگ جهانی دوم موشک کنکور بمب افکن کرونا کووید 19 ویروسبرگهها
جدیدترین یادداشتها
همه- لئونارد اویلر
- بخشهای مختلف هواپیما و کارکرد آنها
- انسان بر لبه انقراض
- ساخت بزرگترین هواپیمای حامل پهباد توسط چین
- چرا تمامی اشکال حیات به اکسیژن وابسته هستند؟
- رایانش کوانتومی چیست؟
- فیلها: بزرگترین حیوانات خشکی
- کاربرد هوش مصنوعی در حل مسایل علمی با Deepseek
- اورکا فرمانروای اقیانوس
- روباتهای انسان نما
- تاریخچه ابداع و ساخت خودرو
- آخرین نئاندرتال
- مروری بر سبک های مختلف نقاشی
- نوآوری در حل تست های ریاضی
- بازی بزرگان: برزیل و فرانسه جام جهانی 1986
بایگانی
- تیر 1404 1
- خرداد 1404 3
- اردیبهشت 1404 1
- فروردین 1404 1
- اسفند 1403 1
- بهمن 1403 2
- دی 1403 1
- آذر 1403 1
- مهر 1403 1
- شهریور 1403 3
- مرداد 1403 1
- تیر 1403 3
- خرداد 1403 4
- اردیبهشت 1403 3
- فروردین 1403 2
- اسفند 1402 7
- بهمن 1402 2
- دی 1402 3
- آذر 1402 3
- آبان 1402 2
- مهر 1402 5
- شهریور 1402 4
- مرداد 1402 12
- تیر 1402 12
- خرداد 1402 5
- اردیبهشت 1402 6
- فروردین 1402 8
- اسفند 1401 6
- بهمن 1401 9
- دی 1401 2
- آذر 1401 3
- آبان 1401 1
- مهر 1401 1
- شهریور 1401 4
- مرداد 1401 7
- تیر 1401 12
- خرداد 1401 10
- اردیبهشت 1401 12
- فروردین 1401 4
- اسفند 1400 4
- بهمن 1400 7
- دی 1400 2
- آبان 1400 5
- مهر 1400 9
- شهریور 1400 1
- مرداد 1400 3
- تیر 1400 6
- خرداد 1400 7
- اردیبهشت 1400 8
- فروردین 1400 7
- اسفند 1399 12
- بهمن 1399 11
- دی 1399 1
- آذر 1399 7
- آبان 1399 2
- مهر 1399 1
- اردیبهشت 1399 7
- فروردین 1399 33
- اسفند 1398 13
- بهمن 1398 9
- دی 1398 1
- خرداد 1398 4
- اردیبهشت 1398 7
- بهمن 1397 5
- دی 1397 5
- آذر 1397 2
- آبان 1397 3
- مهر 1397 3
- شهریور 1397 1
- مرداد 1397 7
- تیر 1397 7
- خرداد 1397 2
- اردیبهشت 1397 6
- اسفند 1396 3
- بهمن 1396 5
- دی 1396 4
- آذر 1396 8
- آبان 1396 6
- مهر 1396 5
- شهریور 1396 6
- مرداد 1396 10
- تیر 1396 9
- خرداد 1396 5
- اردیبهشت 1396 3
- فروردین 1396 8
- اسفند 1395 3
- بهمن 1395 3
- دی 1395 1
- آذر 1395 4
- آبان 1395 2
- مهر 1395 7
- شهریور 1395 5
- مرداد 1395 1
- تیر 1395 3
- خرداد 1395 1
- اردیبهشت 1395 1
- فروردین 1395 3
- اسفند 1394 8
- بهمن 1394 2
- دی 1394 1
- آذر 1394 3
- آبان 1394 2
- مهر 1394 1
- مرداد 1394 1
- تیر 1394 2
- فروردین 1394 1
- اسفند 1393 4
- بهمن 1393 2
- دی 1393 1
- آبان 1393 1
- شهریور 1393 1
- مرداد 1393 1
- تیر 1393 3
- اردیبهشت 1393 7
- فروردین 1393 1
- اسفند 1392 2
- بهمن 1392 8
- دی 1392 6
- آذر 1392 16
- آبان 1392 14
- مهر 1392 19
- شهریور 1392 17
- مرداد 1392 6
- تیر 1392 2
- خرداد 1392 5
- اردیبهشت 1392 9
- فروردین 1392 1
- اسفند 1391 5
- بهمن 1391 8
- دی 1391 6
- آذر 1391 8
- آبان 1391 5
- مهر 1391 12
- شهریور 1391 7
- مرداد 1391 2
- تیر 1391 6
- خرداد 1391 7
- اردیبهشت 1391 8
- فروردین 1391 13
- اسفند 1390 7
- بهمن 1390 6
- دی 1390 11
- آذر 1390 2
- آبان 1390 6
- مهر 1390 4
- شهریور 1390 5
- مرداد 1390 8
- تیر 1390 15
- خرداد 1390 25
- اردیبهشت 1390 11
- فروردین 1390 1
- اسفند 1389 13
- بهمن 1389 12
- دی 1389 5
- آذر 1389 3
- آبان 1389 6
- مهر 1389 7
- شهریور 1389 6
- خرداد 1389 1
- اردیبهشت 1389 3
- اسفند 1388 7
- بهمن 1388 10
- دی 1388 11
- آذر 1388 7
- آبان 1388 17
- آذر 1387 1
- آبان 1387 9
- مهر 1387 5
- شهریور 1387 1
- مرداد 1387 3
- تیر 1387 7
- خرداد 1387 5
- اردیبهشت 1387 1
- فروردین 1387 3
- اسفند 1386 3
- بهمن 1386 9
- دی 1386 19
- آذر 1386 19
- آبان 1386 7
تقویم
تیر 1404| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
جستجو
لئونارد اویلر
بزرگترین ریاضیدان تمامی اعصار
لئونارد اویلر (1707 – 1783) برترین دانشمند سویسی و یکی از سه " اَ بَر ریاضیدان" تاریخ بوده است (دو تن دیگر عبارتند از گاوس و ریمان).
او را شاید بتوان پرکارترین نویسنده تمامی زمانها در هر زمینهای دانست. از 1727 تا 1783 تالیفات او به شکل سیلابی سهمگین تمامی زمینههای علوم را درنوردید و بطور پیوسته ای بر دانش انسانی در هر شاخه ای از ریاضیات محض و کاربردی افزود. همچنین بسیاری زمینه های جدید در ریاضیات ابداع شخص اوست.
او سالانه بطور متوسط 800 صفحه اثر علمی به چاپ میرسانید و همواره بنظر می رسید چیزی ارزشمند برای گفتن دارد و هیچگاه ذهنش از تکاپو نمی ایستاد. انتشار آثار او در سال 1911 آغاز شد و هنوز برای پآن پایانی متصور نیست. قرار بود این نسخه از آثار او شامل 887 عنوان در 72 مجلد باشد اما از آن زمان دست نوشته های ناشناخته جدیدی از او کشف شده و تخمین زده می شود 100 کتاب بزرگ برای تکمیل آثار او مورد نیاز باشد. اویلر آثار ریاضی خود را با آسانی و تسلط یک سخنران ماهر به تحریر در میآورد که در حال صحبت درباره موضوعی آشنا است. نوشته های او مدلی از روشنی و وضوح کامل هستند. او هیچگاه ایده های سرشار خود را خلاصه بیان نمی کرد. فیزیکدان فرانسوی آراگو درباره توانایی های محاسباتی او گفته است: او بدون تلاش آشکاری محاسبات خود را انجام می داد، به آسانی تنفس یک انسان یا پرواز عقاب در آسمان. او در 17 سال آخر عمر خود کاملا نابینا بود با این وجود به مدد حافظه باورنکردنی و تصور نیرومندد خود و کمک اطرافیان توانست به نوشتن کتاب ها و مقالات علمی خود ا دامه دهد و حتی بر حجم آثار خود افزود.
اویلر شهروند باسل و دانشجوی جان برنولی در دانشگاه این شهر بود اما بزودی بر استاد خود برتری یافت. زندگی کاری او به عنوان عضوی از آکادمی علوم در برلین و سنت پترزبورگ گذشت و بیشتر مقالات او در نشریات این موسسات انتشار یافت. او در فیزیولوژی، پزشکی، گیاهشناسی، جغرافیا و کل علوم فیزیکی شناخته شده زمان خود نیز سرآمد بود. زندگانی آرام و بدون حادثهای را گذراند که ثمره آن خانوادهای با سیزده فرزند بود.
به حق گفته اند که تمامی متون درسی مقدماتی و پیشرفته حساب دیفرانسیل و انتگرال نسخه برداری از آثار اویلر بوده است. او هندسه مسطحه و هندسی تحلیلی اجسام صلب را به کمال رساند، رویکرد تحلیلی به مثلثات را ابداع کردو توابع مدرن لگاریتم و تابع نمایی را بسط داد. او نظریه جامعی برای لگاریتم اعداد منفی و موهومی ارائه کرد. اعداد e، پی و i توسط او متداول شدند و معادله معروفی که این سه عدد را به هم پیوند می دهد، یعنی زیباترین معادله دنیای ریاضیات را معرفی کرد:
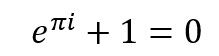
بدون معادله معروف او
یعنی 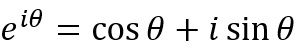 آنالیز پیشرفته وجود نداشت. نمادهای مثلثاتی sin x،
cos x و استفاده از f(x) برای نشان دادن شکل عمومی تابع از دیگر ابداعات درخشان اوست.
آنالیز پیشرفته وجود نداشت. نمادهای مثلثاتی sin x،
cos x و استفاده از f(x) برای نشان دادن شکل عمومی تابع از دیگر ابداعات درخشان اوست.
او نخستین و بزرگترین استاد سریهای نامتناهی، حاصل ضربهای نامتناهی و کسرهای پیوسته بود. حتی جیمز برنولی بزرگ نتوانست مجموع سری نامتناهی زیر را بیابد:
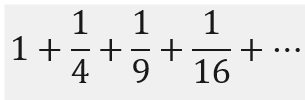
این اویلر بود که
ثابت کرد مجموع فوق برابر 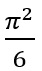
![]() است. او همچنین مجموع های دشوار زیر را اثبات
نمود:
است. او همچنین مجموع های دشوار زیر را اثبات
نمود:
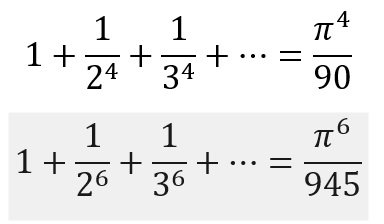
او نخستین کسی بود که کاربرد تبدیلات لاپلاس در حل معادلات دیفرانسیل را تشریح کرد. نظریه مدرن اعداد بیش از همه مدیون کارهای اویلر است.
اطلاع از اهمیت و نقش لویلر در ریاضیات مدرن خود نیاز به تخصص عالی در این زمینه دارد. علاقمندان برای مطالعه بیشتر می توانند به کتاب معادلات دیفرانسیل تالیف سیمونز مراجعه نمایند.
عدد شگفت انگیز اویلر
عدد اویلر e که یک عدد اعشاری بی انتها و نزدیک به 2.71828 است، بطور طبیعی در گستره شگفت انگیزی از محیط زیست بشری خود را مینمایاند. معادلات حاوی e رفتار متغیرهای دنیای واقعی در زیست شناسی، آمار و مهندسی را بازتاب می دهند.
این عدد برای اولین بار در سال 1683 ظهور یافت، زمانی که ژاکوب برنولی استاد دانشگاه بازل سرگرم مطالعه معادلات سود مرکب بود. او می خواست بداند اگر یک بانک روی یک وام یک دلاری، 100 درصد نرخ سود سالانه مرکب به تعداد نامحدود در سال اخذ کند چه اتفاقی خواهد افتاد. عددی که او پیدا کرد همان e بود. معادله ای که برنولی به آن دست یافت به قرار زیر بود:
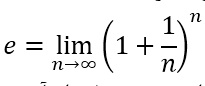
لئونارد اویلر ریاضیدان بزرگ در سال 1731 نام e را بر این عدد نهاد. از آن پس این عدد خود را در مهمترین معادلات احتمال، آمار، مهندسی، زیست شناسی، ترمودینامیک و فیزیک نشان داده است.
"تصور کنید 100 نفر در یک مهمانی شرکت یابند و همگی کت خود را به رخت آویز بیاویزند. فرض کنید هنگام رفتن میزبان به هر نفر بطور تصادفی یک کت بدهد احتمال اینکه هیچ کس کت خود را دریافت نکند با افزایش تعداد افراد به عدد 1/e نزدیک و نزدیکتر می شود".
این عدد همچنین در منحنی های زنگوله ای خود را می نمایاند، منحنی هایی آماری درباره متغیرهای تصادفی که به یکدیگر اضافه می شوند. معادله اساسی یک منحنی زنگوله ای به قرار زیر است:
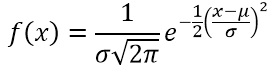
که در آن متغیرها عبارتند از:

عدد e در معادلات مربوط به تعیین سن ارگانیسم های زنده با استفاده از کربن 14و تلاشی نمایی مواد رادیواکتیو نیز ظاهر می شود. وقتی یک موجود زنده می میرد، کربن 14 موجود در استخوانهای او شروع به تلاشی می کند. کربن 14 نیمه عمر مشخصی دارد و میزان باقی مانده در استخوان موجود زنده تابع زمانی است که از مرگ آن موجود گذشته است.
بدین ترتیب عدد e را می توان یکی از شگفت انگیزترین اعداد دردنیای ریاضیات دانست.
منبع: Popular Mechanics
زیباترین معادله ریاضیات
معادله زیر به زیباترین معادله در دنیای ریاضیات موسوم است:
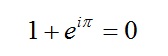
زیبایی این معادله علاوه بر سادگی آن در عین پیچیدگی، از آن جهت است که سه ثابت اساسی در ریاضیات یعنی عدد پی، عدد اویلر و ریشه عدد 1- را به هم پیوند می دهد.اثبات این معادله با توجه به فرمول
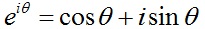
به سادگی معلوم می گردد.
____________________________________________________________________________________
تدریس خصوصی دروس ریاضیات دبیرستان و دانشگاه
توسط مهندس مکانیک با بیش از بیست سال سابقه تدریس
مبتکر روشهای نوآورانه حل پرسش های چهارگزینه ای ریاضی
و دوره آموزشی خلاقیت در ریاضیات
دروس:
ریاضیات دبیرستان، حساب دیفرانسیل و انتگرال، ریاضیات گسسته،
محاسبات عددی، ریاضیات مهندسی، معادلات دیفرانسیل
جزوات مدون و مکتوب و نمونه سوالات امتحانی در اختیار فراگیران قرار خواهد گرفت.
شماره تماس: 09360771981
____________________________________________
خودآموز ریاضیات تجربی برای داوطلبان کنکور

این کتاب تجربه ای نو در آموزش ریاضیات دبیرستان به افرادی است که فرصت محدودی برای مطالعه دارند و می خواهند بدون نیاز به دبیر، ریاضیات را بصورت اصولی و عمیق فرا گیرند.علاوه بر داوطلبان کنکور، همگی دانش آموزان رشته تجربی نیز می توانند از این کتاب به عنوان منبع درسی استفاده کنند. ساختار موضوعی متفاوت کتاب و حجم بسیار مفید آن، مانع خستگی و سردرگمی خواننده می شود و او را در دریایی از مسایل غامض و دشوار رها نمی کند.
کتاب حاصل سالها تجربه تدریس نویسنده است و بازخوردهای مفیدی از سوی دانش آموزان دریافت کرده است.
در صورت تمایل به خرید این خودآموز به صورت فایل PDF با شماره 09360771981 از طریق واتس آپ پیام بفرستید.
بها: 25 هزار تومان
ارسال از طریق واتس آپ، تلگرام یا ایمیل