
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبر
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبردرباره من
دستهها
- تصاویر جالب علمی 60
- اخبار علمی 116
- تاریخ علم 21
- مقالات علمی 187
- حقایق علمی 29
- پرسش و پاسخ علمی 4
- تکنولوژی نظامی 170
- مشاهیر 11
- معرفی وبسایت علمی 10
- سخن بزرگان 4
- تفریح و سرگرمی 1
- شگفتیهای طبیعت 6
- مسابقه علمی 6
- زبان انگلیسی 18
- دیرین شناسی 35
- مهندسی مکانیک 56
- دنیای ریاضیات 54
- فایل های قابل دانلود 8
- پزشکی و سلامت 88
- ترین ها 38
- کنکور 1390 14
- نمونه سوال امتحانی و آزمون 20
- معرفی نرم افزار 4
- واژه نامههای تخصصی 1
- آزمایش های ساده و جالب فیزیک 4
- کنکور 13
- تکنولوژی نفت و حفاری 5
- بانک مقالات علمی 3
- آیرودینامیک و پرواز 6
- استانداردهای مهندسی 6
- محیط زیست 39
- باستان شناسی 5
- پروژه درسی و سمینار 5
- برنامه نویسی کامپیوتر 11
- رپرتاژ آگهی 1
ابر برجسب
کووید 19 کرونا ویروس ریاضیات جنگنده هواپیما ستاره زمین لرزه گرمایش جهانی F-35 موشک کنکور بمب افکن سیاهچاله جنگ جهانی دومبرگهها
جدیدترین یادداشتها
همه- کوارک ها: اجزای سازنده ماده
- آموزش زبان برنامه نویسی پایتون با مثال
- سمی ترین حیوانات طبیعت
- کهن ترین مجسمه ساخت انسان
- راه حل اویلر برای مساله بازل
- ژنتیک: چگونه ویژگیهای خود را از نیاکان به ارث میبریم؟
- برنارد ریمان، آفریدگار هندسه نا اقلیدسی
- ابتذال چیست؟ ریشه آن کدام است؟
- اتمها از کجا آمدهاند؟
- پیری: با گذشت عمر چه اتفاقی برای بدن می افتد؟
- مسایل حل شده از معادلات دیفرانسیل
- لئونارد اویلر
- بخشهای مختلف هواپیما و کارکرد آنها
- انسان بر لبه انقراض
- ساخت بزرگترین هواپیمای حامل پهباد توسط چین
بایگانی
- آبان 1404 2
- مهر 1404 3
- شهریور 1404 3
- مرداد 1404 2
- تیر 1404 2
- خرداد 1404 3
- اردیبهشت 1404 1
- فروردین 1404 1
- اسفند 1403 1
- بهمن 1403 2
- دی 1403 1
- آذر 1403 1
- مهر 1403 1
- شهریور 1403 3
- مرداد 1403 1
- تیر 1403 3
- خرداد 1403 4
- اردیبهشت 1403 3
- فروردین 1403 2
- اسفند 1402 7
- بهمن 1402 2
- دی 1402 3
- آذر 1402 3
- آبان 1402 2
- مهر 1402 5
- شهریور 1402 4
- مرداد 1402 12
- تیر 1402 12
- خرداد 1402 5
- اردیبهشت 1402 6
- فروردین 1402 8
- اسفند 1401 6
- بهمن 1401 9
- دی 1401 2
- آذر 1401 3
- آبان 1401 1
- مهر 1401 1
- شهریور 1401 4
- مرداد 1401 7
- تیر 1401 12
- خرداد 1401 10
- اردیبهشت 1401 12
- فروردین 1401 4
- اسفند 1400 4
- بهمن 1400 7
- دی 1400 2
- آبان 1400 5
- مهر 1400 9
- شهریور 1400 1
- مرداد 1400 3
- تیر 1400 6
- خرداد 1400 7
- اردیبهشت 1400 8
- فروردین 1400 7
- اسفند 1399 12
- بهمن 1399 11
- دی 1399 1
- آذر 1399 7
- آبان 1399 2
- مهر 1399 1
- اردیبهشت 1399 7
- فروردین 1399 33
- اسفند 1398 13
- بهمن 1398 9
- دی 1398 1
- خرداد 1398 4
- اردیبهشت 1398 7
- بهمن 1397 5
- دی 1397 5
- آذر 1397 2
- آبان 1397 3
- مهر 1397 3
- شهریور 1397 1
- مرداد 1397 7
- تیر 1397 7
- خرداد 1397 2
- اردیبهشت 1397 6
- اسفند 1396 3
- بهمن 1396 5
- دی 1396 4
- آذر 1396 8
- آبان 1396 6
- مهر 1396 5
- شهریور 1396 6
- مرداد 1396 10
- تیر 1396 9
- خرداد 1396 5
- اردیبهشت 1396 3
- فروردین 1396 8
- اسفند 1395 3
- بهمن 1395 3
- دی 1395 1
- آذر 1395 4
- آبان 1395 2
- مهر 1395 7
- شهریور 1395 5
- مرداد 1395 1
- تیر 1395 3
- خرداد 1395 1
- اردیبهشت 1395 1
- فروردین 1395 3
- اسفند 1394 8
- بهمن 1394 2
- دی 1394 1
- آذر 1394 3
- آبان 1394 2
- مهر 1394 1
- مرداد 1394 1
- تیر 1394 2
- فروردین 1394 1
- اسفند 1393 4
- بهمن 1393 2
- دی 1393 1
- آبان 1393 1
- شهریور 1393 1
- مرداد 1393 1
- تیر 1393 3
- اردیبهشت 1393 7
- فروردین 1393 1
- اسفند 1392 2
- بهمن 1392 8
- دی 1392 6
- آذر 1392 16
- آبان 1392 14
- مهر 1392 19
- شهریور 1392 17
- مرداد 1392 6
- تیر 1392 2
- خرداد 1392 5
- اردیبهشت 1392 9
- فروردین 1392 1
- اسفند 1391 5
- بهمن 1391 8
- دی 1391 6
- آذر 1391 8
- آبان 1391 5
- مهر 1391 12
- شهریور 1391 7
- مرداد 1391 2
- تیر 1391 6
- خرداد 1391 7
- اردیبهشت 1391 8
- فروردین 1391 13
- اسفند 1390 7
- بهمن 1390 6
- دی 1390 11
- آذر 1390 2
- آبان 1390 6
- مهر 1390 4
- شهریور 1390 5
- مرداد 1390 8
- تیر 1390 15
- خرداد 1390 25
- اردیبهشت 1390 11
- فروردین 1390 1
- اسفند 1389 13
- بهمن 1389 12
- دی 1389 5
- آذر 1389 3
- آبان 1389 6
- مهر 1389 7
- شهریور 1389 6
- خرداد 1389 1
- اردیبهشت 1389 3
- اسفند 1388 7
- بهمن 1388 10
- دی 1388 11
- آذر 1388 7
- آبان 1388 17
- آذر 1387 1
- آبان 1387 9
- مهر 1387 5
- شهریور 1387 1
- مرداد 1387 3
- تیر 1387 7
- خرداد 1387 5
- اردیبهشت 1387 1
- فروردین 1387 3
- اسفند 1386 3
- بهمن 1386 9
- دی 1386 19
- آذر 1386 19
- آبان 1386 7
تقویم
آبان 1404| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
جستجو
نگاهی به کتاب های درسی نظام جدید آموزشی
خدا بیامرزدش. در همسایگی مان پیر زن خوش زبانی زندگی می کرد به نام نرگس خانم. اصالتا اهل دماوند بود و با آنکه حتی سواد خواندن و نوشتن نداشت گاهی ضرب المثل های شیرینی می گفت که در هیچ کتاب ادبی نمی شد پیدا کرد. خیلی از اوقات می گفت: "نکرده کارو نگیرین بکار" که بر اهمیت تجربه و به قول معروف پیرهن پاره کردن در گذر زمان تاکید داشت. تجربه و تعهد وقتی با هم همراه می شوند می توانند نتایج بزرگی ببار داشته باشند.
سالیان سال در این مرز و بوم کار تالیف کتبهای درسی به عهده برخی از فرهیخته ترین دانشمندان این سرزمین گذاشته شده بود. مانند دکتر حسین گل گلاب دانشمند بزرگ زیست شناسی، واژه پرداز بزرگ و سراینده شعر جاودان ای ایران ای مرز پرگهر. گذشت و گذشت تا نوبت ایام به گروههایی جدید رسید که گویا تالیف کتابهای درسی را بیشتر به عنوان یک پروژه نگاه می کردند تا خلق یک اثر ماندگار. مانند عزیزانی که تجربه خود در تالیف را از نوشتن جزوات دانشگاهی یا کمک درسی فراگرفته بودند!
برای نقد کتابهای درسی نظام جدید لازم نیست خیلی موشکافانه وارد قضیه شویم. کافی است نگاهی به عنوان و سرفصلهای کتاب حسابان سال سوم ریاضی بیاندازیم. یعنی کتابی که نقش مهمی در شکل دادن به ذهن دانش آموز و آماده ساختن او برای ورود به دنیای ریاضیات مدرن دارد.
نام کتاب "حسابان" است، یعنی "دو حساب". اما کدام دو حساب؟ منظور حساب دیفرانسیل و حساب انتگرال است که زیربنای ریاضیات نوین محسوب می شود. اما با مطالعه کتاب می بینید که تنها گذری به حساب دیفرانسیل شده است و از حساب انتگرال خبری نیست! بخش اول کتاب هم به جبران مافات و ارائه نواقص سالهای گذشته اختصاص داده شده است!
بنابراین نام کتاب غلط است و از ابتدا مولفین کتاب با یک اشتباه صریح کار را شروع کرده اند: خشت اول چون نهد معمار کج.... کتاب حسابان فقط از یک نوع حساب صحبت می کند و نام حسابان یا دو حساب برای آن درست نیست.
راستی چه اتفاقی افتاده است؟ تالیف کتاب درسی باید یک امر مقدس تلقی شود نه کاری از روی رفع مسئولیت. کتابهای درسی خوب می توانند آینده نسل جوان را متحول کنند. نوجوانی که بهترین مونس او کتاب درسی اوست کمتر به دام انحرافات اخلاقی و فکری می افتد و خلاق تر و مسئولیت پذیرتر بار می آید. مولفین کتابهای درسی نظام جدید هیگاه تحقیق کرده اند چند نفر از دانش آموزان ما کتاب درسی را به عنوان یک منبع قابل اعتماد برای یادگیری می داند؟ مطمئنم پاسخی برای این سوال ندارند.
الگوهای جالب اعداد
به چند الگوی جالب اعداد که در زیر معرفی شده توجه کنید. آیا میتوانید توضیحی برای آنها بیابید؟
الگوی اول:
12345679 x 9 = 111,111,111
12345679 x 18 = 222,222,222
12345679 x 27 = 333,333,333
12345679 x 36 = 444,444,444
12345679 x 45 = 555,555,555
12345679 x 54 = 666,666,666
12345679 x 63 = 777,777,777
12345679 x 72 = 888,888,888
12345679 x 81 = 999,999,999
دقت کنید که عامل های دوم ضرب، مضارب عدد نه هستند و رقم 8 از دنباله ارقام 12345679 غایب است.
الگوی دوم:
1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321
الگوی سوم:
0 x 9 + 1 = 1
1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
الگوی چهارم:
0 x 9 + 8 = 8
9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
آخرین قضیه فرما
پیر فرما (تولد 1601) بنیان گذار نظریه نوین اعداد محسوب می شود. سالهایی از دهه 1630 زندگی او وقف تصحیح کتاب آریثماتیکا اثر کلاسیک دیوفانتوس شده بود. او در حاشیه این کتاب مطلبی یادداشت کرد که به مدت چهارصدسال ریاضی دانان پس از خود را به تکاپو واداشت.
این مطلب پیرامون قضیه ای بود که اکنون به عنوان آخرین قضیه فرما شناخته می شود. مطابق این قضیه معادله دیوفانتین یعنی 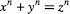 برای n > 2 در مجموعه اعداد صحیح جواب ندارد. به عنوان مثال هیچ سه عدد صحیح مخالف صفر را نمیتوان یافت که معادله x3 + y3 = z3 را برآورده سازد.
برای n > 2 در مجموعه اعداد صحیح جواب ندارد. به عنوان مثال هیچ سه عدد صحیح مخالف صفر را نمیتوان یافت که معادله x3 + y3 = z3 را برآورده سازد.
توجه کنید که برای n=2 معادله به فرم x2+y2 = z2 در میآید که همان قضیه فیثاغورث است و می دانیم بیشمار سه تایی صحیح میتوان پیدا کرد که در معادله فوق صدق کنند.
فرما در حاشیه کتاب ادعا کرد که اثبات این قضیه را یافته است. لیکن از ذکر آن خودداری کرد. اکنون تقریبا مطمئنیم که ادعای فرما خیلی دقیق نبوده و احتمالا برای n=3 و n=4 این قضیه را ثابت کرده، لیکن حل عمومی آن را نیافته است.
در سال 1993 انفجاری در عالم ریاضیات اتفاق افتاد. اندرو وایلز با اثبات حالت نیمه پایدار حدس تانی یاما-شیمورا قضیه فرما را بطور پارهای اثبات کرد. متاسفانه رخنههای متعددی در روش اثبات اندرو وایلز پدیدار شد. لیکن در سال 1994 وایلز و تایلور با همکاری هم مسئله را به یک فرمول شماره رده (Class Number Forula) فرو کاسته و اثبات نهایی آخرین قضیه فرما را ارائه کردند.
اثبات قضیه فرما پایان یک دوران در ریاضیات بود. از آن جایی که ابزارهای مورد استفاده در حل این مسئله هنوز در زمان فرما ابداع نشده بودند، بنظر می رسد حل ادعایی فرما واقعیت نداشته باشد.
در یکی از اپیزودهای کارتون معروف The Simpsons، معادله 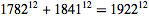 در نقطه ای از پس زمینه تصویر دیده می شود. ممکن است بنظر برسد که این اعداد به ازای n=12 در قضیه فرما صدق میکنند، در حالی که حاصل دو طرف تنها در نه رقم اول با یکدیگر تطابق دارد.
در نقطه ای از پس زمینه تصویر دیده می شود. ممکن است بنظر برسد که این اعداد به ازای n=12 در قضیه فرما صدق میکنند، در حالی که حاصل دو طرف تنها در نه رقم اول با یکدیگر تطابق دارد.

منابعی برای مطالعه بیشتر:
http://mathworld.wolfram.com/FermatsLastTheorem.html
حدس گولدباخ
به تساویهای زیر دقت کنید:
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7
12 = 5 + 7
14 = 7 + 7
16 = 5 + 11
18 = 7 + 11
20 = 7 + 13
22 = 5 + 17
24 = 7 + 17
...
به نظر می رسد هر عدد زوج بزرگتر از 2 را میتوان بصورت مجموع دو عدد اول نوشت. آیا این امر برای تمام اعداد زوج بزرگتر از 2 امکان پذیر است؟ اولین بار کریستین گولدباخ دانشمند نظریه اعداد (1690 تا 1764 میلادی) این نظریه را مطرح کرد. تلاش دانشمندان برای اثبات این مسئله هنوز به نتیجه نرسیده است!
دو قلوهای اول
دوقلوهای اول یا prime twines ، یک جفت عدد اول هستند که 2 واحد با یکدیگر تقاوت دارند. چند مثال از این جفت اعداد عبارتند از (3,5)، (11,13) و (1000000007,1000000009). بزرگترین دو قلوی اول شناخته شده عبارتند از:
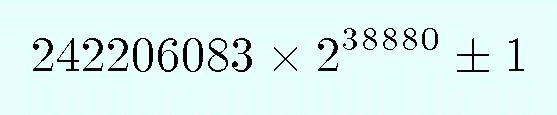
هرکدام از اعداد فوق 11713 رقم دارند. چه تعداد از این جفت اعداد اول وجود دارد؟ آیا تعداد این جفت اعداد اول محدود است یا نامحدود؟ هنوز کسی پاسخ این پرسشها را نمیداند!
منبع: