
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبر
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبردرباره من
دستهها
- تصاویر جالب علمی 60
- اخبار علمی 116
- تاریخ علم 21
- مقالات علمی 187
- حقایق علمی 29
- پرسش و پاسخ علمی 4
- تکنولوژی نظامی 170
- مشاهیر 11
- معرفی وبسایت علمی 10
- سخن بزرگان 4
- تفریح و سرگرمی 1
- شگفتیهای طبیعت 6
- مسابقه علمی 6
- زبان انگلیسی 18
- دیرین شناسی 35
- مهندسی مکانیک 56
- دنیای ریاضیات 54
- فایل های قابل دانلود 8
- پزشکی و سلامت 88
- ترین ها 38
- کنکور 1390 14
- نمونه سوال امتحانی و آزمون 20
- معرفی نرم افزار 4
- واژه نامههای تخصصی 1
- آزمایش های ساده و جالب فیزیک 4
- کنکور 13
- تکنولوژی نفت و حفاری 5
- بانک مقالات علمی 3
- آیرودینامیک و پرواز 6
- استانداردهای مهندسی 6
- محیط زیست 39
- باستان شناسی 5
- پروژه درسی و سمینار 5
- برنامه نویسی کامپیوتر 11
- رپرتاژ آگهی 1
ابر برجسب
کووید 19 کرونا ویروس ریاضیات جنگنده هواپیما ستاره زمین لرزه گرمایش جهانی F-35 موشک کنکور بمب افکن سیاهچاله جنگ جهانی دومبرگهها
جدیدترین یادداشتها
همه- کوارک ها: اجزای سازنده ماده
- آموزش زبان برنامه نویسی پایتون با مثال
- سمی ترین حیوانات طبیعت
- کهن ترین مجسمه ساخت انسان
- راه حل اویلر برای مساله بازل
- ژنتیک: چگونه ویژگیهای خود را از نیاکان به ارث میبریم؟
- برنارد ریمان، آفریدگار هندسه نا اقلیدسی
- ابتذال چیست؟ ریشه آن کدام است؟
- اتمها از کجا آمدهاند؟
- پیری: با گذشت عمر چه اتفاقی برای بدن می افتد؟
- مسایل حل شده از معادلات دیفرانسیل
- لئونارد اویلر
- بخشهای مختلف هواپیما و کارکرد آنها
- انسان بر لبه انقراض
- ساخت بزرگترین هواپیمای حامل پهباد توسط چین
بایگانی
- آبان 1404 2
- مهر 1404 3
- شهریور 1404 3
- مرداد 1404 2
- تیر 1404 2
- خرداد 1404 3
- اردیبهشت 1404 1
- فروردین 1404 1
- اسفند 1403 1
- بهمن 1403 2
- دی 1403 1
- آذر 1403 1
- مهر 1403 1
- شهریور 1403 3
- مرداد 1403 1
- تیر 1403 3
- خرداد 1403 4
- اردیبهشت 1403 3
- فروردین 1403 2
- اسفند 1402 7
- بهمن 1402 2
- دی 1402 3
- آذر 1402 3
- آبان 1402 2
- مهر 1402 5
- شهریور 1402 4
- مرداد 1402 12
- تیر 1402 12
- خرداد 1402 5
- اردیبهشت 1402 6
- فروردین 1402 8
- اسفند 1401 6
- بهمن 1401 9
- دی 1401 2
- آذر 1401 3
- آبان 1401 1
- مهر 1401 1
- شهریور 1401 4
- مرداد 1401 7
- تیر 1401 12
- خرداد 1401 10
- اردیبهشت 1401 12
- فروردین 1401 4
- اسفند 1400 4
- بهمن 1400 7
- دی 1400 2
- آبان 1400 5
- مهر 1400 9
- شهریور 1400 1
- مرداد 1400 3
- تیر 1400 6
- خرداد 1400 7
- اردیبهشت 1400 8
- فروردین 1400 7
- اسفند 1399 12
- بهمن 1399 11
- دی 1399 1
- آذر 1399 7
- آبان 1399 2
- مهر 1399 1
- اردیبهشت 1399 7
- فروردین 1399 33
- اسفند 1398 13
- بهمن 1398 9
- دی 1398 1
- خرداد 1398 4
- اردیبهشت 1398 7
- بهمن 1397 5
- دی 1397 5
- آذر 1397 2
- آبان 1397 3
- مهر 1397 3
- شهریور 1397 1
- مرداد 1397 7
- تیر 1397 7
- خرداد 1397 2
- اردیبهشت 1397 6
- اسفند 1396 3
- بهمن 1396 5
- دی 1396 4
- آذر 1396 8
- آبان 1396 6
- مهر 1396 5
- شهریور 1396 6
- مرداد 1396 10
- تیر 1396 9
- خرداد 1396 5
- اردیبهشت 1396 3
- فروردین 1396 8
- اسفند 1395 3
- بهمن 1395 3
- دی 1395 1
- آذر 1395 4
- آبان 1395 2
- مهر 1395 7
- شهریور 1395 5
- مرداد 1395 1
- تیر 1395 3
- خرداد 1395 1
- اردیبهشت 1395 1
- فروردین 1395 3
- اسفند 1394 8
- بهمن 1394 2
- دی 1394 1
- آذر 1394 3
- آبان 1394 2
- مهر 1394 1
- مرداد 1394 1
- تیر 1394 2
- فروردین 1394 1
- اسفند 1393 4
- بهمن 1393 2
- دی 1393 1
- آبان 1393 1
- شهریور 1393 1
- مرداد 1393 1
- تیر 1393 3
- اردیبهشت 1393 7
- فروردین 1393 1
- اسفند 1392 2
- بهمن 1392 8
- دی 1392 6
- آذر 1392 16
- آبان 1392 14
- مهر 1392 19
- شهریور 1392 17
- مرداد 1392 6
- تیر 1392 2
- خرداد 1392 5
- اردیبهشت 1392 9
- فروردین 1392 1
- اسفند 1391 5
- بهمن 1391 8
- دی 1391 6
- آذر 1391 8
- آبان 1391 5
- مهر 1391 12
- شهریور 1391 7
- مرداد 1391 2
- تیر 1391 6
- خرداد 1391 7
- اردیبهشت 1391 8
- فروردین 1391 13
- اسفند 1390 7
- بهمن 1390 6
- دی 1390 11
- آذر 1390 2
- آبان 1390 6
- مهر 1390 4
- شهریور 1390 5
- مرداد 1390 8
- تیر 1390 15
- خرداد 1390 25
- اردیبهشت 1390 11
- فروردین 1390 1
- اسفند 1389 13
- بهمن 1389 12
- دی 1389 5
- آذر 1389 3
- آبان 1389 6
- مهر 1389 7
- شهریور 1389 6
- خرداد 1389 1
- اردیبهشت 1389 3
- اسفند 1388 7
- بهمن 1388 10
- دی 1388 11
- آذر 1388 7
- آبان 1388 17
- آذر 1387 1
- آبان 1387 9
- مهر 1387 5
- شهریور 1387 1
- مرداد 1387 3
- تیر 1387 7
- خرداد 1387 5
- اردیبهشت 1387 1
- فروردین 1387 3
- اسفند 1386 3
- بهمن 1386 9
- دی 1386 19
- آذر 1386 19
- آبان 1386 7
تقویم
آبان 1404| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
جستجو
روشهای ابتکاری تست زدن (8)
در همسایگی محذوف متقارن (3a-7 , a+5) – {3} شعاع همسایگی کدام است؟ (کنکور سراسری ریاضی 1389)
حل) طبق تعریف همسایگی محذوف بایدفاصله دو انتهای بازه از مرکز آن یعنی x = 3 یکسان باشد، پس:
(a+5) - 3 = 3 - (3a-7) --> a = 2
پس همسایگی به شکل (-1,7) - {3} در می آید. شعاع همسایگی برابر است با 7-3 = 4 یا 3-(-1) = 4 پس گزینه 4 صحیح است.
نکته ای مهم درباره آمادگی داوطلب در جلسه برگزاری کنکور
به ازای کدام مقادیر a منحنی به معادله y=ax2-(a+2)x از ناحیه دوم محورهای مختصات نمی گذرد؟ (کنکور سراسری ریاضی 1389)
حل) منحنی مزبور از مبدا مختصات می گذرد. اگر بخواهیم چنین سهمی از ناحیه دوم نگذرد باید شکلی بصورت زیر داشته باشد:
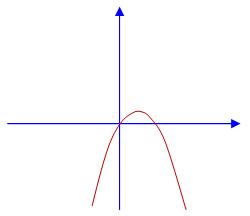
بنابراین معادله مزبور باید دارای یک ریشه مثبت باشد در ضمن باید a<0 ، زیرا شاخه های منحنی رو به پایین است. در نتیجه خواهیم داشت:
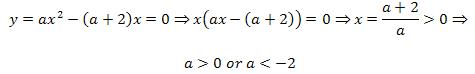
از طرفی باید a<0 بنابراین جواب نهایی a<-2 خواهد بود که در گزینه ها موجود نیست.
متاسفانه این تست که هر چهارگزینه آن غلط است به عنوان اولین تست ریاضی کنکور سراسری سال 1389 در برگه سوالات آمده است. برای تایید این مطلب می توانید به جزوات گروه مهندس عربشاهی یا سایر موسسات آموزشی مراجعه کنید.
اما خطر اصلی که یک داوطلب را در هنگام برخورد با یک تست غلط تهدید می کند از دست دادن وقت و شوک روانی ناشی از این مطلب یا جابجا زدن تست هاست. در این گونه موارد باید داوطلب ضمن تسلط بر خویش روی هر تست بیش از زمان استاندارد وقت نگذارد و اگر تستی را جواب نمی دهد، با یک علامت در پاسخنامه آنرا مشخص کند تا احیانا پاسخ تست بعدی را در آن محل علامت نزند.
روشهای ابتکاری تست زدن (5)
دو تابع با ضابطه های f(x) = [x]+[-x] و g(x) = x2+x-2 مفروض اند. اگر g(f(x)) = -2 مجموعه مقادیر x کدام است؟ (کنکور سراسری ریاضی 1389)
1) R-Z 2) Z 3) R 4) ø
حل: این تست با توجه به یکی از خواص تابع جزء صحیح براحتی حل می شود. طبق تعریف داریم:
اگر x یک عدد صحیح باشد [x]+[-x]=0 و اگر یک عدد غیر صحیح باشد [x]+[-x] = -1. بنابراین:
x عدد صحیح -> f(x) = 0 -> g(f(x)) = g(0) = -2
x عدد غیرصحیح -> f(x) = -1 -> g(f(x)) = g(-1) = -2
بنابراین در هرحالت g(f(x)) = -2 و گزینه 3 صحیح است.


