
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبر
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبردرباره من
دستهها
- تصاویر جالب علمی 60
- اخبار علمی 115
- تاریخ علم 21
- مقالات علمی 183
- حقایق علمی 29
- پرسش و پاسخ علمی 4
- تکنولوژی نظامی 170
- مشاهیر 10
- معرفی وبسایت علمی 10
- سخن بزرگان 4
- تفریح و سرگرمی 1
- شگفتیهای طبیعت 6
- مسابقه علمی 6
- زبان انگلیسی 18
- دیرین شناسی 34
- مهندسی مکانیک 56
- دنیای ریاضیات 51
- فایل های قابل دانلود 8
- پزشکی و سلامت 88
- ترین ها 36
- کنکور 1390 14
- نمونه سوال امتحانی و آزمون 20
- معرفی نرم افزار 4
- واژه نامههای تخصصی 1
- آزمایش های ساده و جالب فیزیک 4
- کنکور 13
- تکنولوژی نفت و حفاری 5
- بانک مقالات علمی 3
- آیرودینامیک و پرواز 6
- استانداردهای مهندسی 6
- محیط زیست 38
- باستان شناسی 5
- پروژه درسی و سمینار 5
- برنامه نویسی کامپیوتر 10
- رپرتاژ آگهی 1
ابر برجسب
جنگنده هواپیما ریاضیات ستاره زمین لرزه گرمایش جهانی F-35 سیاهچاله جنگ جهانی دوم موشک کنکور بمب افکن کرونا کووید 19 ویروسبرگهها
جدیدترین یادداشتها
همه- لئونارد اویلر
- بخشهای مختلف هواپیما و کارکرد آنها
- انسان بر لبه انقراض
- ساخت بزرگترین هواپیمای حامل پهباد توسط چین
- چرا تمامی اشکال حیات به اکسیژن وابسته هستند؟
- رایانش کوانتومی چیست؟
- فیلها: بزرگترین حیوانات خشکی
- کاربرد هوش مصنوعی در حل مسایل علمی با Deepseek
- اورکا فرمانروای اقیانوس
- روباتهای انسان نما
- تاریخچه ابداع و ساخت خودرو
- آخرین نئاندرتال
- مروری بر سبک های مختلف نقاشی
- نوآوری در حل تست های ریاضی
- بازی بزرگان: برزیل و فرانسه جام جهانی 1986
بایگانی
- تیر 1404 1
- خرداد 1404 3
- اردیبهشت 1404 1
- فروردین 1404 1
- اسفند 1403 1
- بهمن 1403 2
- دی 1403 1
- آذر 1403 1
- مهر 1403 1
- شهریور 1403 3
- مرداد 1403 1
- تیر 1403 3
- خرداد 1403 4
- اردیبهشت 1403 3
- فروردین 1403 2
- اسفند 1402 7
- بهمن 1402 2
- دی 1402 3
- آذر 1402 3
- آبان 1402 2
- مهر 1402 5
- شهریور 1402 4
- مرداد 1402 12
- تیر 1402 12
- خرداد 1402 5
- اردیبهشت 1402 6
- فروردین 1402 8
- اسفند 1401 6
- بهمن 1401 9
- دی 1401 2
- آذر 1401 3
- آبان 1401 1
- مهر 1401 1
- شهریور 1401 4
- مرداد 1401 7
- تیر 1401 12
- خرداد 1401 10
- اردیبهشت 1401 12
- فروردین 1401 4
- اسفند 1400 4
- بهمن 1400 7
- دی 1400 2
- آبان 1400 5
- مهر 1400 9
- شهریور 1400 1
- مرداد 1400 3
- تیر 1400 6
- خرداد 1400 7
- اردیبهشت 1400 8
- فروردین 1400 7
- اسفند 1399 12
- بهمن 1399 11
- دی 1399 1
- آذر 1399 7
- آبان 1399 2
- مهر 1399 1
- اردیبهشت 1399 7
- فروردین 1399 33
- اسفند 1398 13
- بهمن 1398 9
- دی 1398 1
- خرداد 1398 4
- اردیبهشت 1398 7
- بهمن 1397 5
- دی 1397 5
- آذر 1397 2
- آبان 1397 3
- مهر 1397 3
- شهریور 1397 1
- مرداد 1397 7
- تیر 1397 7
- خرداد 1397 2
- اردیبهشت 1397 6
- اسفند 1396 3
- بهمن 1396 5
- دی 1396 4
- آذر 1396 8
- آبان 1396 6
- مهر 1396 5
- شهریور 1396 6
- مرداد 1396 10
- تیر 1396 9
- خرداد 1396 5
- اردیبهشت 1396 3
- فروردین 1396 8
- اسفند 1395 3
- بهمن 1395 3
- دی 1395 1
- آذر 1395 4
- آبان 1395 2
- مهر 1395 7
- شهریور 1395 5
- مرداد 1395 1
- تیر 1395 3
- خرداد 1395 1
- اردیبهشت 1395 1
- فروردین 1395 3
- اسفند 1394 8
- بهمن 1394 2
- دی 1394 1
- آذر 1394 3
- آبان 1394 2
- مهر 1394 1
- مرداد 1394 1
- تیر 1394 2
- فروردین 1394 1
- اسفند 1393 4
- بهمن 1393 2
- دی 1393 1
- آبان 1393 1
- شهریور 1393 1
- مرداد 1393 1
- تیر 1393 3
- اردیبهشت 1393 7
- فروردین 1393 1
- اسفند 1392 2
- بهمن 1392 8
- دی 1392 6
- آذر 1392 16
- آبان 1392 14
- مهر 1392 19
- شهریور 1392 17
- مرداد 1392 6
- تیر 1392 2
- خرداد 1392 5
- اردیبهشت 1392 9
- فروردین 1392 1
- اسفند 1391 5
- بهمن 1391 8
- دی 1391 6
- آذر 1391 8
- آبان 1391 5
- مهر 1391 12
- شهریور 1391 7
- مرداد 1391 2
- تیر 1391 6
- خرداد 1391 7
- اردیبهشت 1391 8
- فروردین 1391 13
- اسفند 1390 7
- بهمن 1390 6
- دی 1390 11
- آذر 1390 2
- آبان 1390 6
- مهر 1390 4
- شهریور 1390 5
- مرداد 1390 8
- تیر 1390 15
- خرداد 1390 25
- اردیبهشت 1390 11
- فروردین 1390 1
- اسفند 1389 13
- بهمن 1389 12
- دی 1389 5
- آذر 1389 3
- آبان 1389 6
- مهر 1389 7
- شهریور 1389 6
- خرداد 1389 1
- اردیبهشت 1389 3
- اسفند 1388 7
- بهمن 1388 10
- دی 1388 11
- آذر 1388 7
- آبان 1388 17
- آذر 1387 1
- آبان 1387 9
- مهر 1387 5
- شهریور 1387 1
- مرداد 1387 3
- تیر 1387 7
- خرداد 1387 5
- اردیبهشت 1387 1
- فروردین 1387 3
- اسفند 1386 3
- بهمن 1386 9
- دی 1386 19
- آذر 1386 19
- آبان 1386 7
تقویم
تیر 1404| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
جستجو
هفت معادله ریاضی که جهان را تغییر دادند
معادلات ریاضی پنجرههایی یکتا به جهان میگشایند. آنها واقعیت را قابل فهم کرده و به ما کمک میکنند امور نامشهود را ببینیم. بنابراین شگفتی ندارد که ابداعات جدید در ریاضیات پا به پای پیشرفت ما در فهم عالم گسترش یابند. در این مقاله هفت معادله تاریخی معرفی میشوند که در نگرش ما از ریزترین ذرات تا تمامی گستره کیهان انقلابی ایجاد کردند.
منبع: Live Science
نظریه فیثاغورث
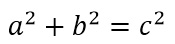
یکی از کهن ترین معادلات اصلی مثلثات که همه دانش آموزان در مدرسه یاد میگیرند، رابطه میان طول سه ضلع یک مثلث قائم الزاویه است: مجموع مربعات دو ضلع قائم مثلث راست گوشه، برابر مربع ضلع سوم (وتر) است. این معادله از 3700 سال پیش یعنی دوره زندگی بابلیان باستان شناخته شده است.
اعتبار نگاشتن این معادله به شکل امروزین خود، به نام ریاضی دان یونانی فیثاغورس ثبت شده است. نظریه فیثاغورس علاوه بر ساخت و ساز، ناوبری، نقشه کشی و سایر زمینه های مهم، در توسعه نظریه اعداد بسیار موثر بوده است. در سده پنجم میلادی هیپارکوس متاپونتام خاطرنشان ساخت که وتر یک مثلث راست گوشه با طول ضلع 1، برابر جدر عدد 2 است که عددی ناگویا است. گفته میشود هیپارکوس به خاطر این کشف به دریا انداخته شد زیرا طرفداران متعصب فیثاغورس از ابراز وجود اعداد ناگویا که ارقام اعشاری غیرتکراری بی پایان دارند بر آشفته بودند.
قانون دوم نیوتن و قانون گرانش
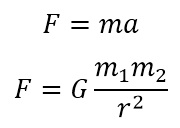
سر آیزاک نیوتن با کشفیاتی که دنیا را تکان داد مشهور است. در زمره آنها، قانون دوم حرکت است که بیان میدارد نیروی وارد بر جسم با حاصل ضرب جرم در شتاب آن برابر است. بسط این قانون همراه با مشهدات دیگر او را به سوی قانون عمومی گرانش در سال 1687 رهنمون شد. G در این قانون یک ثابت بنیادی است که مقدار آن بر اساس تجربیات آزمایشگاهی تعیین شد. از این مفاهیم برای درک بسیاری دستگاه های فیزیکی از جمله حرکت سیارات به دور خورشید و سفر میان آنها با موشک های ساخت بشر استفاده شده است.
معادله موج
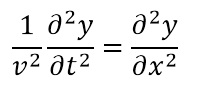
با استفاده از قوانین نیوتن، دانشمندان قرن هجده شروع به تحلیل تمامی پدیده های عالم کردند. در 1743 ریاضیدان فرانسوی ژان باپتیست له رون دالامبر معادله ای استخراج کرد که ارتعاشات یک سیم نوسان کننده یا حرکت موج را تشریح می کرد. دراین معادله v سرعت موج و سایر پارامترها توصیف کننده جابجایی موج در یک جهت هستند. با بسط این معادله به دو و سه بعد دانشمندان توانستند حرکت امواج آب، زمین لرزه و امواج صوتی را پیش بینی کنند. این معادله مبنای معادله شرودینگر در فیزیک کوانتم نیز گردید که زیربنای بسیاری از فناوریهای کامپیوتری است.
معادلات فوریه
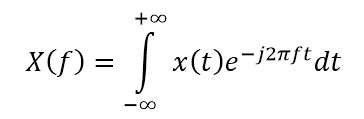
اگر حتی نام دانشمند فرانسوی ژان باپتیست ژوزف فوریه را نشنیده باشید کارهای او بر زندگی شما تاثیر گذارده است. معادلات ریاضی ابداع شده توسط او در سال 1822 به پژوهشگران امکان داد داده های پیچیده و آشفته را به ترکیبی از امواج ساده که تحلیلی آنها بسیار آسانتر است فروکاهند. تبدیل فوریه، نمادی بنیادین در زمان خود بود. این ابزار ریاضی در بسیاری از زمین های نوین علوم از جمله پردازش داده، تحلیل تصاویر، نورشناسی، ارتباطات، نجوم و مهندسی کاربرد یافته و توانسته سیستم های پیچیده را به بخش های ساده تر شکسته و قابل تحلیل نماید.
معادلات ماکسول
در اوایل سده 1800 الکتریسیته و مغناطیس هنوز مفاهیم جدیدی بوده و دانشمندان در جستجوی روشی برای تسخیر و لگام زدن به این نیروهای شگفت بودند. دانشمند اسکاتلندی جیمز کلرک ماکسول با انتشار فهرستی از 20 معادله در سال 1864 درک ما از این دو پدیده را بسیار ارتقا بخشید و رابطه میان آن دو را معلوم کرد. این معادلات بعدا به شکل 4 معادله عمومی ترکیب شدند و بنیان الکترونیک در عصر فناوری های نوین را تشکیل میدهند.
قانون جرم و انرژی اینشتاین
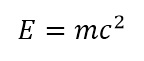
این معادله کوچک یکی از مشهورترین در دنیای علون نوین است. این معادله که برای اولین بار در 1905 توسط آلبرت اینشتاین بیان شد، بخشی از نظریه ساختارشکن نسبیت خاص بوده و نشان میدهد که ماده و انرژی دو جنبه مختلف یک واقعیت هستند. بدون این قانون امکان درک سازوکار تابش انرژی توسط ستارگان و ساختن شتاب دهنده های عظیم ذرات برای درک دنیا یزیراتمی وجود نداشت.
معادلات فریدمن
ممکن است ابداع معادلاتی که بتوانند کل کیهان را تعریف کنند بسیار مغرورانه بنظر برسد اما این همان کاری است که فیزیکدان روسی الکساندر فریدمن در دهه 1920 انجام داد. با استفاده از نظریات نسبیت اینشتاین او نشان داد که ویژگی های یک عالم در حال انبساط می توانند با استفاده از دو معادله از زمان انفجار مهبانگ (Big Bang) به بعدتوضیح داده شوند.
این معادلات تمامی ویژگی های عالم از جمله انحنای آن، میزان ماده و انرژی موجود در آن، سرعت انبساط آن و تعداد ثابت های مهم کیهانی را با هم ترکیب می کنند. سرعت نور، ثابت گرانش و ثابت هابل که شتاب انبساط عالم را تعیین می کند از این جمله هستند. مشهور است که اینشتاین ایده عالم در حال انبساط یا انقباض را دوست نداشت اما نظریه نسبیت عام او برپایه اثر گرانش این طور پیش بینی می کرد. او ثابتی به نماد لامبدا به معادلات خود افزود تا با اثر گرانش مقابله کرده و عاملی ایستا نتیجه دهد. در حالی که او این کار خود را بزرگترین اشتباهش نامید، چند دهه بعد ثابت شد چنین ثابتی واقعا وجود دارد و به فرض وجود ماده تاریک در عالم می انجامد که موجبات یک عالم با شتاب انبساطی فزاینده را ایجاب کرده است.