
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبر
دنیای علم و تکنولوژی
اخبار و مقالات مربوط به دنیای علم و تکنولوژی ترجمه شده از منابع معتبردرباره من
دستهها
- تصاویر جالب علمی 60
- اخبار علمی 116
- تاریخ علم 21
- مقالات علمی 187
- حقایق علمی 29
- پرسش و پاسخ علمی 4
- تکنولوژی نظامی 170
- مشاهیر 11
- معرفی وبسایت علمی 10
- سخن بزرگان 4
- تفریح و سرگرمی 1
- شگفتیهای طبیعت 6
- مسابقه علمی 6
- زبان انگلیسی 18
- دیرین شناسی 35
- مهندسی مکانیک 56
- دنیای ریاضیات 54
- فایل های قابل دانلود 8
- پزشکی و سلامت 88
- ترین ها 38
- کنکور 1390 14
- نمونه سوال امتحانی و آزمون 20
- معرفی نرم افزار 4
- واژه نامههای تخصصی 1
- آزمایش های ساده و جالب فیزیک 4
- کنکور 13
- تکنولوژی نفت و حفاری 5
- بانک مقالات علمی 3
- آیرودینامیک و پرواز 6
- استانداردهای مهندسی 6
- محیط زیست 39
- باستان شناسی 5
- پروژه درسی و سمینار 5
- برنامه نویسی کامپیوتر 11
- رپرتاژ آگهی 1
ابر برجسب
کووید 19 کرونا ویروس ریاضیات جنگنده هواپیما ستاره زمین لرزه گرمایش جهانی F-35 موشک کنکور بمب افکن سیاهچاله جنگ جهانی دومبرگهها
جدیدترین یادداشتها
همه- کوارک ها: اجزای سازنده ماده
- آموزش زبان برنامه نویسی پایتون با مثال
- سمی ترین حیوانات طبیعت
- کهن ترین مجسمه ساخت انسان
- راه حل اویلر برای مساله بازل
- ژنتیک: چگونه ویژگیهای خود را از نیاکان به ارث میبریم؟
- برنارد ریمان، آفریدگار هندسه نا اقلیدسی
- ابتذال چیست؟ ریشه آن کدام است؟
- اتمها از کجا آمدهاند؟
- پیری: با گذشت عمر چه اتفاقی برای بدن می افتد؟
- مسایل حل شده از معادلات دیفرانسیل
- لئونارد اویلر
- بخشهای مختلف هواپیما و کارکرد آنها
- انسان بر لبه انقراض
- ساخت بزرگترین هواپیمای حامل پهباد توسط چین
بایگانی
- آبان 1404 2
- مهر 1404 3
- شهریور 1404 3
- مرداد 1404 2
- تیر 1404 2
- خرداد 1404 3
- اردیبهشت 1404 1
- فروردین 1404 1
- اسفند 1403 1
- بهمن 1403 2
- دی 1403 1
- آذر 1403 1
- مهر 1403 1
- شهریور 1403 3
- مرداد 1403 1
- تیر 1403 3
- خرداد 1403 4
- اردیبهشت 1403 3
- فروردین 1403 2
- اسفند 1402 7
- بهمن 1402 2
- دی 1402 3
- آذر 1402 3
- آبان 1402 2
- مهر 1402 5
- شهریور 1402 4
- مرداد 1402 12
- تیر 1402 12
- خرداد 1402 5
- اردیبهشت 1402 6
- فروردین 1402 8
- اسفند 1401 6
- بهمن 1401 9
- دی 1401 2
- آذر 1401 3
- آبان 1401 1
- مهر 1401 1
- شهریور 1401 4
- مرداد 1401 7
- تیر 1401 12
- خرداد 1401 10
- اردیبهشت 1401 12
- فروردین 1401 4
- اسفند 1400 4
- بهمن 1400 7
- دی 1400 2
- آبان 1400 5
- مهر 1400 9
- شهریور 1400 1
- مرداد 1400 3
- تیر 1400 6
- خرداد 1400 7
- اردیبهشت 1400 8
- فروردین 1400 7
- اسفند 1399 12
- بهمن 1399 11
- دی 1399 1
- آذر 1399 7
- آبان 1399 2
- مهر 1399 1
- اردیبهشت 1399 7
- فروردین 1399 33
- اسفند 1398 13
- بهمن 1398 9
- دی 1398 1
- خرداد 1398 4
- اردیبهشت 1398 7
- بهمن 1397 5
- دی 1397 5
- آذر 1397 2
- آبان 1397 3
- مهر 1397 3
- شهریور 1397 1
- مرداد 1397 7
- تیر 1397 7
- خرداد 1397 2
- اردیبهشت 1397 6
- اسفند 1396 3
- بهمن 1396 5
- دی 1396 4
- آذر 1396 8
- آبان 1396 6
- مهر 1396 5
- شهریور 1396 6
- مرداد 1396 10
- تیر 1396 9
- خرداد 1396 5
- اردیبهشت 1396 3
- فروردین 1396 8
- اسفند 1395 3
- بهمن 1395 3
- دی 1395 1
- آذر 1395 4
- آبان 1395 2
- مهر 1395 7
- شهریور 1395 5
- مرداد 1395 1
- تیر 1395 3
- خرداد 1395 1
- اردیبهشت 1395 1
- فروردین 1395 3
- اسفند 1394 8
- بهمن 1394 2
- دی 1394 1
- آذر 1394 3
- آبان 1394 2
- مهر 1394 1
- مرداد 1394 1
- تیر 1394 2
- فروردین 1394 1
- اسفند 1393 4
- بهمن 1393 2
- دی 1393 1
- آبان 1393 1
- شهریور 1393 1
- مرداد 1393 1
- تیر 1393 3
- اردیبهشت 1393 7
- فروردین 1393 1
- اسفند 1392 2
- بهمن 1392 8
- دی 1392 6
- آذر 1392 16
- آبان 1392 14
- مهر 1392 19
- شهریور 1392 17
- مرداد 1392 6
- تیر 1392 2
- خرداد 1392 5
- اردیبهشت 1392 9
- فروردین 1392 1
- اسفند 1391 5
- بهمن 1391 8
- دی 1391 6
- آذر 1391 8
- آبان 1391 5
- مهر 1391 12
- شهریور 1391 7
- مرداد 1391 2
- تیر 1391 6
- خرداد 1391 7
- اردیبهشت 1391 8
- فروردین 1391 13
- اسفند 1390 7
- بهمن 1390 6
- دی 1390 11
- آذر 1390 2
- آبان 1390 6
- مهر 1390 4
- شهریور 1390 5
- مرداد 1390 8
- تیر 1390 15
- خرداد 1390 25
- اردیبهشت 1390 11
- فروردین 1390 1
- اسفند 1389 13
- بهمن 1389 12
- دی 1389 5
- آذر 1389 3
- آبان 1389 6
- مهر 1389 7
- شهریور 1389 6
- خرداد 1389 1
- اردیبهشت 1389 3
- اسفند 1388 7
- بهمن 1388 10
- دی 1388 11
- آذر 1388 7
- آبان 1388 17
- آذر 1387 1
- آبان 1387 9
- مهر 1387 5
- شهریور 1387 1
- مرداد 1387 3
- تیر 1387 7
- خرداد 1387 5
- اردیبهشت 1387 1
- فروردین 1387 3
- اسفند 1386 3
- بهمن 1386 9
- دی 1386 19
- آذر 1386 19
- آبان 1386 7
تقویم
آبان 1404| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
جستجو
مسایلی از انتگرال مختلط
مسایلی از انتگرال مختلط
انتخاب و حل: اصغر ناصری
مدرس ریاضیات دروس دانشگاهی
انتگرالهای مختلط علاوه بر کاربرد در علوم مهندسی، راه را برای محاسبه برخی انتگرال های حقیقی به شیوه ای بسیار سادهتر میگشایند. در این مقاله مسایلی از انتگرالهای مختلط طرح و حل شده اند که می توانند در امتحانات ریاضی مهندسی دوره کارشناسی مفید واقع شوند. در هر مورد نظریه ریاضی و فرمول مورد استفاده نیز ذکر شده است.
_____________________________________________________________________________________________________
خودآموز ریاضیات تجربی برای داوطلبان کنکور
این کتاب خودآموز موثری برای افرادی است که می خواهند در مدتی محدود مروری جامع بر ریاضیات تجربی داشته باشند و خود را برای کنکور آماده کنند. این خودآموز شما را از مطالعه کتابهای پرحجم رایج کنکور بی نیاز کرده و با طرح و بحث تست ها و نمونه سوالات مفید، موفقیت شما در درس ریاضی کنکور را تضمین می کند. مطالعه این کتاب به سایر علاقمندان به ریاضیات نیز پیشنهاد می شود.

دانلود 50 صفحه اول (PDF) به صورت رایگان
در صورت تمایل به خرید این خودآموز به صورت فایل PDF با شماره 09360771981 از طریق واتس آپ پیام بفرستید.
بها: 25 هزار تومان
ارسال از طریق واتس آپ، تلگرام یا ایمیل
نمونه مسایل معادلات دیفرانسیل با حل تشریحی
مسایلی از معادلات دیفرانسیل
انتخاب و حل: اصغر ناصری
مدرس ریاضیات دروس دانشگاهی
معادلات دیفرانسیل معمولی (ODE) از مهمترین مباحث ریاضیات دانشگاهی هستند و نقش مهمی در مدلسازی پدیدههای دنیای واقعی دارند. در این مقاله مسایل مهمی از بخش های مختلف این مبحث همراه با حل و بحث ارائه شدهاند. با مرور این مسائل که تقریبا تمامی بخشهای یک دوره مقدماتی معادلات دیفرانسیل را پوشش دادهاند، آمادگی خوبی برای آزمونهای این درس خواهید یافت. به عنوان کتاب مرجع، میتوانید به کتاب معادلات دیفرانسیل تالیف دکتر مسعود نیکوکار مراجعه فرمایید.
دانلود فایل مسایلی از معادلات دیفرانسیل (PDF)
مسایلی از اکسترمم نسبی و مطلق توابع چند متغیره
برای درس ریاضی 2 رشته های مختلف دانشگاه
بدست آوردن اکسترمم نسبی و مطلق یک تابع به کمک دو آزمون مشتق اول و دوم انجام می شود. شکل زیر مفهوم سه نقطه مهم در یک تابع : ماکزیمم نسبی، مینیمم نسبی و نقطه زینی را نشان می دهد.
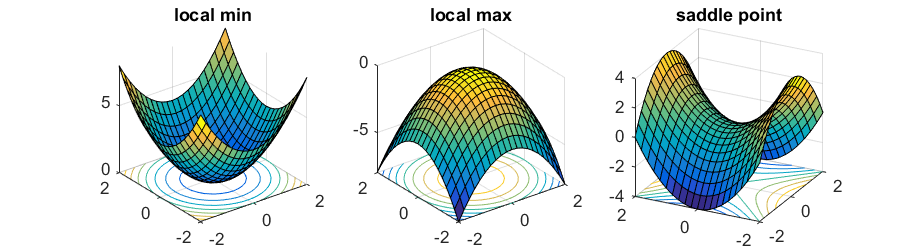
در مقاله کوتاه زیر مثالهایی از این مبحث مهم طرح و حل شده اند.
پوش یک دسته منحنی و طریقه یافتن آن (2)
برای قسمت اول این مقاله کلیک کنید.
مثال: پوش دسته منحنی زیر را بیابید:
(x-c)2+y2=9
َAdvertisement  |  |
حل - این دسته منحنی معرف دوایری به مرکز نقطه (c,0) و شعاع 3 است. برای بدست آوردن پوش دستگاه زیر را حل می کنیم:
f(x,y)=(x-c)2+y2-9=0
fc(x,y)=2(x-c)=0 -> x=c
در معادله دوم نسبت به c مشتق گرفته شده است. اگر در معادله دایره قرار دهیم x=c خواهیم داشت:
(c-c)2+y2=9->y=3 , y=-3
دو خط افقی مزبور معادلات پوش دسته منحنی هستند.شکل زیر نمودار دسته منحنی و پوش آن را نشان می دهد.
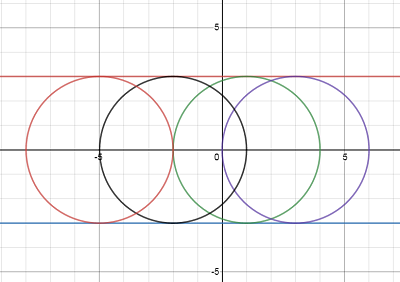
برای ترسیم این نمودار از نرم افزارآانلاین بسیار جالب سایت https://www.desmos.com/calculator استفاده شده است.
حل معادلات دیفرانسیلی که در آن x تابعی از مشتق اول y است.
حل معادلات دیفرانسیل به شکل x=f(y')
معادلاتی از این دست را به سادگی می توان با تغییر متغیر y'=u حل کرد. گاهی اوقات بهتر است 'y را معادل تابعی از u بگیریم. مثال: 
