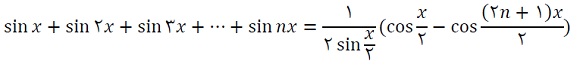
عدد شگفت انگیز اویلر

عدد اویلر e که یک عدد اعشاری بی انتها و نزدیک به 2.71828 است، بطور طبیعی در گستره شگفت انگیزی از محیط زیست بشری خود را می‌نمایاند. معادلات حاوی e رفتار متغیرهای دنیای واقعی در زیست شناسی، آمار و مهندسی را بازتاب می دهند.

این عدد برای اولین بار در سال 1683 ظهور یافت، زمانی که ژاکوب برنولی استاد دانشگاه بازل سرگرم مطالعه معادلات سود مرکب بود. او می خواست بداند اگر یک بانک روی یک وام یک دلاری، 100 درصد نرخ سود سالانه مرکب به تعداد نامحدود در سال اخذ کند چه اتفاقی خواهد افتاد. عددی که او پیدا کرد همان e بود. معادله ای که برنولی به آن دست یافت به قرار زیر بود:

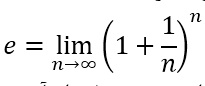
لئونارد اویلر ریاضیدان بزرگ در سال 1731 نام e را بر این عدد نهاد. از آن پس این عدد خود را در مهمترین معادلات احتمال، آمار، مهندسی، زیست شناسی، ترمودینامیک و فیزیک نشان داده است.

"تصور کنید 100 نفر در یک مهمانی شرکت یابند و همگی کت خود را به رخت آویز بیاویزند. فرض کنید هنگام رفتن میزبان به هر نفر بطور تصادفی یک کت بدهد احتمال اینکه هیچ کس کت خود را دریافت نکند با افزایش تعداد افراد به عدد 1/e نزدیک و نزدیکتر می شود".

این عدد همچنین در منحنی های زنگوله ای خود را می نمایاند، منحنی هایی آماری درباره متغیرهای تصادفی که به یکدیگر اضافه می شوند. معادله اساسی یک منحنی زنگوله ای به قرار زیر است:

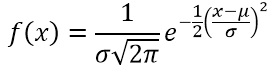
که در آن متغیرها عبارتند از:

عدد e در معادلات مربوط به تعیین سن ارگانیسم های زنده با استفاده از کربن 14و تلاشی نمایی مواد رادیواکتیو نیز ظاهر می شود. وقتی یک موجود زنده می میرد، کربن 14 موجود در استخوانهای او شروع به تلاشی می کند. کربن 14 نیمه عمر مشخصی دارد و میزان باقی مانده در استخوان موجود زنده تابع زمانی است که از مرگ آن موجود گذشته است.

بدین ترتیب عدد e را می توان یکی از شگفت انگیزترین اعداد دردنیای ریاضیات دانست.

منبع: Popular Mechanics

معادلات تابعی

یکی از مسایل جالب آنالیز ریاضی، معادلات تابعی هستند. منظور از یک معادله تابعی، یک تساوی بین مقادیر مختلف یک تابع در آرگومانهای مختلف است. در این نوشتار برای ورود به این مبحث جالب، یک معادله تابعی نمونه را طرح و حل می کنیم.

- تابع f(x) را به گونه ای تعیین کنید که f(x+f(y))=x+y+1

ادامه مطلب

حل و بحث تشریحی امتحان نهایی حسابان 2

حل و بحث تشریحی امتحان نهایی حسابان 2

دیماه 1401

لینک دانلود

مسایلی از انتگرال مختلط

مسایلی از انتگرال مختلط

انتخاب و حل: اصغر ناصری

مدرس ریاضیات دروس دانشگاهی

انتگرال‌های مختلط علاوه بر کاربرد در علوم مهندسی، راه را برای محاسبه برخی انتگرال های حقیقی به شیوه ای بسیار ساده‌تر می‌گشایند. در این مقاله مسایلی از انتگرال‌های مختلط طرح و حل شده اند که می توانند در امتحانات ریاضی مهندسی دوره کارشناسی مفید واقع شوند. در هر مورد نظریه ریاضی و فرمول مورد استفاده نیز ذکر شده است.

دانلود فایل PDF

_____________________________________________________________________________________________________

خودآموز ریاضیات تجربی برای داوطلبان کنکور

این کتاب خودآموز موثری برای افرادی است که می خواهند در مدتی محدود مروری جامع بر ریاضیات تجربی داشته باشند و خود را برای کنکور آماده کنند. این خودآموز شما را از مطالعه کتابهای پرحجم رایج کنکور بی نیاز کرده و با طرح و بحث تست ها و نمونه سوالات مفید، موفقیت شما در درس ریاضی کنکور را تضمین می کند. مطالعه این کتاب به سایر علاقمندان به ریاضیات نیز پیشنهاد می شود.

تعداد صفحات 255

فرمت فایل: PDF

حجم فایل: 7 مگابایت

دانلود 50 صفحه اول (PDF) به صورت رایگان

در صورت تمایل به خرید این خودآموز به صورت فایل PDF با شماره 09360771981 از طریق واتس آپ پیام بفرستید.

بها: 25 هزار تومان

ارسال از طریق واتس آپ، تلگرام یا ایمیل

نمونه مسایل معادلات دیفرانسیل با حل تشریحی

مسایلی از معادلات دیفرانسیل

انتخاب و حل: اصغر ناصری

مدرس ریاضیات دروس دانشگاهی

معادلات دیفرانسیل معمولی (ODE) از مهمترین مباحث ریاضیات دانشگاهی هستند و نقش مهمی در مدلسازی پدیده‌های دنیای واقعی دارند. در این مقاله مسایل مهمی از بخش های مختلف این مبحث همراه با حل و بحث ارائه شده‌اند. با مرور این مسائل که تقریبا تمامی بخش‌های یک دوره مقدماتی معادلات دیفرانسیل را پوشش داده‌اند، آمادگی خوبی برای آزمونهای این درس خواهید یافت. به عنوان کتاب مرجع، می‌توانید به کتاب معادلات دیفرانسیل تالیف دکتر مسعود نیکوکار مراجعه فرمایید.

دانلود فایل مسایلی از معادلات دیفرانسیل (PDF)